
【题目】图1,抛物线与x轴交于A(﹣1,0),B(3,0),顶点为D(1,﹣4),点P为y轴上一动点.
(1)求抛物线的解析式;
(2)在y轴的负半轴上是否存在点P,使△BDP是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(3)如图2,点![]() 在抛物线上,求
在抛物线上,求![]() 的最小值.
的最小值.
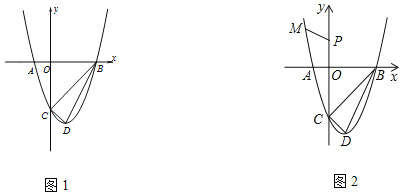
【答案】(1)y=x2﹣2x﹣3;(2)点P坐标为(0,﹣![]() )或(0,﹣
)或(0,﹣![]() ﹣4)或(0,﹣1);(3)
﹣4)或(0,﹣1);(3)![]()
【解析】
(1)由已知抛物线顶点坐标为D,设抛物线的解析式为y=a(x﹣1)2﹣4,再把点A代入即可求得二次项系数a的值,由此即可求得抛物线的解析式;(2)由点B、D坐标可求BD的长.设点P坐标为(0,t),用t表示BP2,DP2.对BP=BD、DP=BD、BP=DP三种情况进行分类讨论计算,解方程求得t的值并讨论是否合理即可;(3)由点B、C坐标可得∠BCO=45°,所以过点P作BC垂线段PQ即构造出等腰直角△PQC,可得PQ=![]() PC,故有MP+
PC,故有MP+![]() PC=MP+PQ.过点M作BC的垂线段MH,根据垂线段最短性质,可知当点M、P、Q在同一直线上时,MP+
PC=MP+PQ.过点M作BC的垂线段MH,根据垂线段最短性质,可知当点M、P、Q在同一直线上时,MP+![]() PC=MP+PQ=MH最小,即需求MH的长.连接MB、MC构造△BCM,利用y轴分成△BCD与△CDM求面积和即得到△BCM面积,再由S△BCM=
PC=MP+PQ=MH最小,即需求MH的长.连接MB、MC构造△BCM,利用y轴分成△BCD与△CDM求面积和即得到△BCM面积,再由S△BCM=![]() BCMH即求得MH的长.
BCMH即求得MH的长.
解:(1)∵抛物线顶点为D(1,﹣4),
∴设抛物线的解析式为y=a(x﹣1)2﹣4,
∵A(﹣1,0)在抛物线上
∴4a﹣4=0,解得:a=1
∴抛物线的解析式为y=(x﹣1)2﹣4=x2﹣2x﹣3
(2)在y轴的负半轴上存在点P,使△BDP是等腰三角形.
∵B(3,0),D(1,﹣4)
∴BD2=(3﹣1)2+(0+4)2=20
设y轴负半轴的点P坐标为(0,t)(t<0)
∴BP2=32+t2,DP2=12+(t+4)2
①若BP=BD,则9+t2=20
解得:t1=![]() (舍去),t2=﹣
(舍去),t2=﹣![]()
②若DP=BD,则1+(t+4)2=20
解得:t1=![]() -4(舍去),t2=﹣
-4(舍去),t2=﹣![]() ﹣4
﹣4
③若BP=DP,则9+t2=1+(t+4)2
解得:t=﹣1
综上所述,点P坐标为(0,﹣![]() )或(0,﹣
)或(0,﹣![]() ﹣4)或(0,﹣1)
﹣4)或(0,﹣1)
(3)连接MC、MB,MB交y轴于点D,过点P作PQ⊥BC于点Q,过点M作MH⊥BC于点H
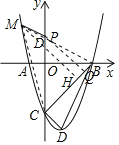
∵x=0时,y=x2﹣2x﹣3=﹣3;
∴C(0,﹣3);
∵B(3,0),∠BOC=90°;
∴∠OBC=∠OCB=45°,BC=3![]()
∵∠PQC=90°
∴Rt△PQC中,sin∠BCO=![]() =
=![]()
∴PQ=![]() PC,
PC,
∴MP+![]() PC=MP+PQ;
PC=MP+PQ;
∵MH⊥BC于点H,
∴当点M、P、Q在同一直线上时,MP+![]() PC=MP+PQ=MH最小,
PC=MP+PQ=MH最小,
∵M(﹣![]() ,m)在抛物线上
,m)在抛物线上
∴m=(﹣![]() )2﹣2×(﹣
)2﹣2×(﹣![]() )﹣3=
)﹣3=![]()
∴M(﹣![]() ,
,![]() )
)
设直线MB解析式为y=kx+b
∴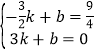 ,
,
解得: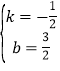 ,
,
∴直线MB:y=﹣![]() x+
x+![]() ,
,
∴MB与y轴交点D(0,![]() ),
),
∴CD=![]() ﹣(﹣3)=
﹣(﹣3)=![]() ,
,
∴S△BCM=S△BCD+S△CDM=![]() CDBO+
CDBO+![]() CD|xM|=
CD|xM|=![]() CD(xB﹣xM)=
CD(xB﹣xM)=![]() ×
×![]() ×(3+
×(3+![]() )=
)=![]() ,
,
∵S△BCM=![]() BCMH,
BCMH,
∴MH=![]() =
=![]() ,
,
∴MP+![]() PC的最小值为
PC的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】小明购买了一套安居型商品房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题:
(1)用含x、y的代数式表示地面总面积;
(2)若x=5,y=![]() ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个粒子在第一象限内及x轴,y轴上运动,第1分钟从原点运动到![]() ,第2分钟从
,第2分钟从![]() 运动到
运动到![]() ,而后它接着按图中箭头所示的与x轴y轴平行的方向来回运动,且每分钟移动1个长度单位.在第2019分钟时,这个粒子所在位置的坐标是( )
,而后它接着按图中箭头所示的与x轴y轴平行的方向来回运动,且每分钟移动1个长度单位.在第2019分钟时,这个粒子所在位置的坐标是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.
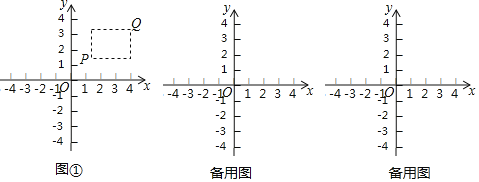
已知点A的坐标为(1,0),
(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=![]() ,AD=2.点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F.当△CDF是等腰三角形时,BE的长为_____.
,AD=2.点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F.当△CDF是等腰三角形时,BE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米?
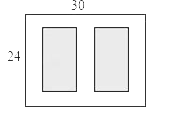
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABC的平分线交AD于点E,过点D作BE的平行线交于BC于F.
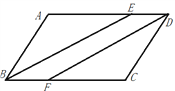
(1)求证:△ABE≌△CDF;
(2)若AB=6,BC=8,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m,水面下降2.5m,水面宽度增加( )
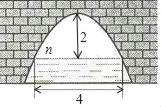
A. 1 m B. 2 m C. 3 m D. 6 m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com