练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．端州区在旧城改造过程中，需要整修一段全长4000m的道路．为了尽量减少施工对城市交通所造成的影响，实际工作效率比原计划提高了25%，结果提前8天完成任务．求原计划每小时修路的长度为多少？

    分析 本题的关键语是：“提前8天完成任务”；等量关系为：原计划用的时间-实际所用的时间=8．而工作时间=工作总量÷工作效率．

    解答 解：设原计划每小时修路的长度为x米，
    依题意得：$\frac{4000}{x}$-$\frac{4000}{（1+25%）x}$=8，

    解得x=100，
    经检验，x=100是所列方程的解．
    答：原计划每小时修路的长度为100米．

    点评 本题考查了分式方程的应用．应用题中一般有三个量，求一个量，明显的有一个量，一定是根据另一量来列等量关系的．本题考查分式方程的应用，分析题意，找到合适的等量关系是解决问题的关键．本题应用的等量关系为：工作时间=工作总量÷工效．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．如图，已知等边三角形ABC中，D为AC边的中点，E为BC延长线上一点，CE=CD，DM⊥BC于M，求证：M是BE的中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列命题中，假命题的是（　　）
    A．分别有一个角是110°的两个等腰三角形相似
    B．如果两个三角形相似，则他们的面积比等于相似比
    C．若5x=8y，则$\frac{x}{y}$=$\frac{8}{5}$
    D．有一个角相等的两个菱形相似

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

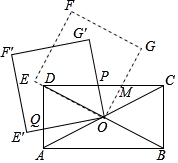    19．如图，矩形ABCD的对角线交于点O，正方形OEFG的一条边OE在直线OD上，OG与CD交于点M，正方形OEFG绕点O逆时针旋转，OG′，OE′分别与CD，AD交于点P，Q．已知矩形长与宽的比值为2，则在旋转过程中PM：DQ=（　　）
    A．1：3B．2：3C．1：2D．3：4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．当分式$\frac{x+2}{x-1}$的值为0时，字母x的取值应为（　　）
    A．-1B．1C．-2D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

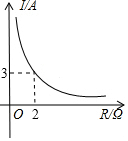    16．已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示．则用电阻R表示电流I的函数表达式为（　　）
    A．$I=\frac{3}{R}$B．$I=-\frac{6}{R}$C．$I=-\frac{3}{R}$D．$I=\frac{6}{R}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

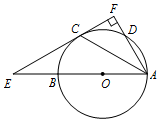    3．如图，AB是⊙O的直径，C，D是⊙O上两点，且$\widehat{BC}$=$\widehat{CD}$，过点C的直线CF⊥AD于点F，交AB的延长线于点E，连接AC．
    （1）求证：EF是⊙O的切线；
    （2）连接FO，若sinE=$\frac{1}{2}$，⊙O的半径为r，请写出求线段FO长的思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

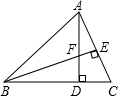    20．如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D，E，AD与BE相交于点F．
    （1）求证：△ACD∽△BFD；
    （2）当$\frac{AD}{BD}$=1，AC=3时，求BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图1，△ABC中，AD是∠BAC的平分线，若AB=AC+CD，那么∠ACB与∠ABC有怎样的数量关系？小明通过观察分析，形成了如下解题思路：

    如图2，延长AC到E，使CE=CD，连接DE．由AB=AC+CD，可得AE=AB．又因为AD是∠BAC的平分线，可得△ABD≌△AED，进一步分析就可以得到∠ACB与∠ABC的数量关系．
    （1）判定△ABD与△AED全等的依据是SAS；
    （2）∠ACB与∠ABC的数量关系为：∠ACB=2∠ABC．

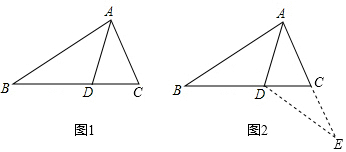
    查看答案和解析>>

    同步练习册答案