
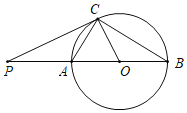
【题目】如图,已知AB是⊙O的直径,AC是弦,点P是BA延长线上一点,连接PC、BC,∠PCA=∠B.
(1)求证:PC是⊙O的切线;
(2)若PC=4,PA=2,求直径AB的长.
【答案】(1)见解析;(2)AB=6.
【解析】
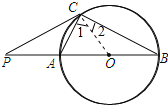
(1)连接OC,由圆周角定理得出∠ACB=90°,得出∠1+∠2=90°,由等腰三角形的性质得出∠PCA=∠2,因此∠1+∠PCA=90°,即PC⊥OC,即可得出结论
(2)由切割线定理得出PC![]() =PA
=PA![]() PB,求出PB,即可得出直径AB的长解答
PB,求出PB,即可得出直径AB的长解答
(1)证明:连接OC,如图所示:
∵AB是⊙的直径,
∴∠ACB=90°,
即∠1+∠2=90°,
∵OB=OC,
∴∠2=∠B,
又∵∠PCA=∠B,
∴∠PCA=∠2,
∴∠1+∠PCA=90°,
即PC⊥OC,
∴PC是⊙O的切线;
(2)解:∵PC是⊙O的切线,
∴PC2=PAPB,
∴42=2×PB,
解得:PB=8,
∴AB=PB﹣PA=8﹣2=6.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1长为半径画弧,交直线y=![]() x于点B1.过点B1作B1A2∥y轴交直线y=2x于点A2,以O为圆心,OA2长为半径画弧,交直线y═
x于点B1.过点B1作B1A2∥y轴交直线y=2x于点A2,以O为圆心,OA2长为半径画弧,交直线y═![]() x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3,以点O为圆心,OA3长为半径画弧,交直线y=
x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3,以点O为圆心,OA3长为半径画弧,交直线y=![]() x于点B3;……按如此规律进行下去,点B2020的坐标为_____.
x于点B3;……按如此规律进行下去,点B2020的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学以致用:问题1:怎样用长为![]() 的铁丝围成一个面积最大的矩形?
的铁丝围成一个面积最大的矩形?
小学时我们就知道结论:围成正方形时面积最大,即围成边长为![]() 的正方形时面积最大为
的正方形时面积最大为![]() .请用你所学的二次函数的知识解释原因.
.请用你所学的二次函数的知识解释原因.
思考验证:问题2:怎样用铁丝围一个面积为![]() 且周长最小的矩形?
且周长最小的矩形?
小明猜测:围成正方形时周长最小.
为了说明其中的道理,小明翻阅书籍,找到下面的结论:
在![]() 、
、![]() 均为正实数)中,若
均为正实数)中,若![]() 为定值
为定值![]() ,则
,则![]() ,只有当
,只有当![]() 时,
时,![]() 有最小值
有最小值![]() .
.
思考验证:证明:![]() 、
、![]() 均为正实数)
均为正实数)
请完成小明的证明过程:
证明:对于任意正实数![]() 、
、![]()
![]()
![]()
![]()
解决问题:
(1)若![]() ,则
,则![]() (当且仅当
(当且仅当![]() 时取“
时取“![]() ”
” ![]() ;
;
(2)运用上述结论证明小明对问题2的猜测;
(3)填空:当![]() 时,
时,![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
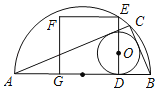
【题目】如图,AB为半圆的直径,C是半圆弧上一点,正方形DEFG的一边DG在直径AB上,另一边DE过△ABC的内切圆圆心O,且点E在半圆上.
(1)当正方形的顶点F也在半圆弧上时,半圆的半径与正方形边长的比为 ;
(2)当正方形DEFG的面积为100,且△ABC的内切圆⊙O的半径r=4,求半圆的直径AB的值;
(3)若半圆的半径为R,直接写出⊙O半径r可取得的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
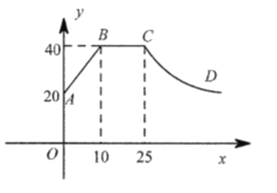
【题目】一般情况下,学生注意力上课后逐渐增强,中间有段时间处于较理想的稳定状态,随后开始分散.实验结果表明,学生注意力指数y随时间x(min)的变化规律如图所示(其中![]() 分别为线段,
分别为线段,![]() 为双曲线的一部分):
为双曲线的一部分):
(1)上课后第![]() 与第
与第![]() 相比较,何时学生注意力更集中?
相比较,何时学生注意力更集中?
(2)某道难题需连续讲![]() ,为保证效果,学生注意力指数不宜低于
,为保证效果,学生注意力指数不宜低于![]() ,老师能否在所需要求下讲完这道题?
,老师能否在所需要求下讲完这道题?
查看答案和解析>>
科目:初中数学 来源: 题型:
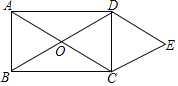
【题目】如图,矩形ABCD对角线AC、BD交于点O,边AB=6,AD=8,四边形OCED为菱形,若将菱形OCED绕点O旋转一周,旋转过程中OE与矩形ABCD的边的交点始终为M,则线段ME的长度可取的整数值为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的半径为
的半径为![]() ,点
,点![]() 与圆心
与圆心![]() 不重合,给出如下定义:若在
不重合,给出如下定义:若在![]() 上存在一点
上存在一点![]() ,使
,使![]() ,则称点
,则称点![]() 为
为![]() 的特征点.
的特征点.
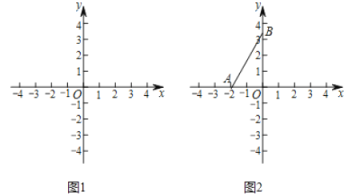
(1)当![]() 的半径为1时,如图1.
的半径为1时,如图1.
①在点![]() ,
,![]() ,
,![]() 中,
中,![]() 的特征点是__________.
的特征点是__________.
②点![]() 在直线
在直线![]() 上,若点
上,若点![]() 为
为![]() 的特征点,求
的特征点,求![]() 的取值范围.
的取值范围.
(2)如图2,![]() 的圆心在
的圆心在![]() 轴上,半径为2,点
轴上,半径为2,点![]() ,
,![]() .若线段
.若线段![]() 上的所有点都是
上的所有点都是![]() 的特征点,直接写出圆心
的特征点,直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com