
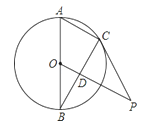
【题目】如图,AB为⊙O的直径,D为弦BC的中心,连接OD并延长交过点C的切线于点P,连接AC.求证:△CPD∽△ABC.
科目:初中数学 来源: 题型:
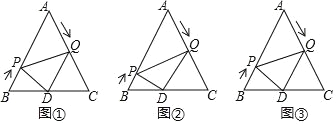
【题目】如图,已知△ABC是边长为6cm的等边三角形,动点P,Q同时从B,A两点出发,分别沿BA,AC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P,Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)如图①,当t为何值时,AP=3AQ;
(2)如图②,当t为何值时,△APQ为直角三角形;
(3)如图③,作 QD∥AB交 BC于点D,连接PD,当t为何值时,△BDP与△PDQ相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
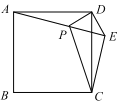
【题目】如图,在正方形![]() 外取一点
外取一点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() .若
.若![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③点
;③点![]() 到直线
到直线![]() 的距离为
的距离为![]() ;④
;④![]() ;⑤
;⑤![]() 正方形
正方形![]() .其中正确的是( )
.其中正确的是( )
A.①②③④B.①②④⑤C.①③④D.①②⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班五位同学参加学校举办的数学竞赛,试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分。赛后A,B, C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表:
参赛同学 | 答对题数 | 答错题数 | 未答题数 |
A | 19 | 0 | 1 |
B | 17 | 2 | 1 |
C | 15 | 2 | 3 |
D | 17 | 1 | 2 |
E | / | / | 7 |
(1)根据以上信息,求A,B,C,D四位同学成绩的平均分;
(2)最后获知:A,B,C,D,E五位同学成绩分别是95分,81分,64分,83分,58分.
①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况.请指出哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山种植某产品种蜜柚![]() 已知该蜜柚的成本价为8元
已知该蜜柚的成本价为8元![]() 千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量
千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量![]() 千克
千克![]() 与销售单价
与销售单价![]() 元
元![]() 千克
千克![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
![]() 求y与x的函数关系式,并写出x的取值范围;
求y与x的函数关系式,并写出x的取值范围;
![]() 当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.
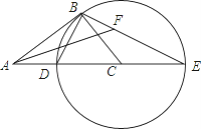
(1)求证:△ABD∽△AEB;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=2,求⊙C的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC、AB交于点D、E.
(1)在图中作出AB的垂直平分线DE,并连接BD.
(2)证明:△ABC∽△BDC.
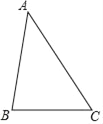
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com