
【题目】如图,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(1)如果点![]() 在底边
在底边![]() 上且以
上且以![]() 的速度由
的速度由![]() 点向
点向![]() 点运动,同时点
点运动,同时点![]() 在腰
在腰![]() 上由
上由![]() 向
向![]() 点运动.
点运动.
①如果点![]() 与点
与点![]() 的运动速度相等,求经过多少秒后
的运动速度相等,求经过多少秒后![]() ;
;
②如果点![]() 与点
与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() 与
与![]() 全等?
全等?
(2)若点![]() 以②中的运动速度从点
以②中的运动速度从点![]() 出发,点
出发,点![]() 以
以![]() 速度从点
速度从点![]() 同时出发,都逆时针沿
同时出发,都逆时针沿![]() 三边运动,直接写出当点
三边运动,直接写出当点![]() 与点
与点![]() 第一次相遇时
第一次相遇时![]() 的运动的路程.
的运动的路程.
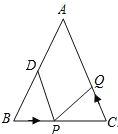
【答案】(1)①经过1秒;②![]() ;(2)160cm
;(2)160cm
【解析】
(1)①先求得BM=CN=6,MC=BD=10,然后根据等边对等角求得∠B=∠C,最后根据SAS即可证明;
②因为VM≠VN,所以BM≠CN,又∠B=∠C,要使△BMD与△CNM全等,只能BM=CM=8,根据全等得出CN=BD=10,然后根据运动速度求得运动时间,根据时间和CN的长即可求得N的运动速度;
(2)因为VN>VM,只能是点N追上点M,即点N比点M多走AB+AC的路程,据此列出方程,解这个方程即可求得.
(1)①设经过![]() 秒后
秒后![]() ,由题意可得
,由题意可得![]() ,
,
∴![]() ,
,
∴![]() ,在
,在![]() 和
和![]() 中,
中,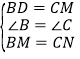 ,
,
∴![]() ,
,
∴经过1秒后![]() ;
;
设经过![]() 秒后
秒后![]() ,记
,记![]() 两点的速度分别为
两点的速度分别为![]() ,
,
∴![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
此时要使![]() 和
和![]() 全等,则
全等,则![]() ,
,
∴![]() ;
;
当![]() 时,若
时,若![]() ,则
,则![]() 中任一边长均比
中任一边长均比![]() 长,
长,
∴![]() 和
和![]() 不可能全等;
不可能全等;
若![]() ,则
,则![]() 中任一边长均比
中任一边长均比![]() 短,
短,
∴![]() 和
和![]() 不可能全等;
不可能全等;
综上所述,当![]() 时,
时,![]() .
.
(2)因为VN>VM,只能是点N追上点M,即点N比点M多走AB+AC的路程,
设经过x秒后M与N第一次相遇,
依题意得![]() x=6x+2×20,
x=6x+2×20,
解得x=![]() (秒)
(秒)
此时点M运动了![]() ×6=160(cm)
×6=160(cm)
故点![]() 与点
与点![]() 第一次相遇时点
第一次相遇时点![]() 运动路径为
运动路径为![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知 A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)请在图中作出△ABC 关于 y 轴对称的△![]() ,并求出△
,并求出△![]() 的面积;
的面积;
(2)写出 ![]() 、
、![]() 的坐标
的坐标 ![]() __________;
__________;![]() __________;
__________;
(3)若△DBC 与△ABC 全等,则 D 的坐标为_____.
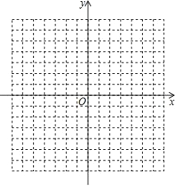
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发沿同一路线驶向B地,甲车匀速驶向B地,甲车出发30分钟后,乙车才出发,乙先匀速行驶一段时间后,到达货站装货后继续行驶,速度减少了56千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法中正确的是( ) 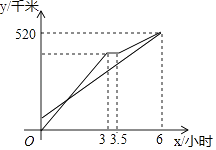
A.甲车从A地到B地行驶了6小时
B.甲的速度是120千米/时
C.乙出发90分钟追上甲
D.当两车在行驶过程中,相距40千米时,x=2或3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2开始,连续的偶数相加,它们和的情况如表:
加数的个数n | S |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=15=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
(1)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=;
(2)如下数表是由从1开始的连续自然数组成,观察规律:
①第n行的第一个数可用含n的式子表示为;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,DC∥AB,BD平分∠ABC,CD=4.
(1)求BC的长;
(2)如图2,若∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.请判断△DEF的形状并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AD长为6,AB是弦,∠A=30°,CD∥AB,且CD= ![]() .
. 
(1)求∠C的度数;
(2)求证:BC是⊙O的切线;
(3)求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
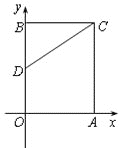
【题目】如图,在平面直角坐标系中,长方形![]() 的顶点
的顶点![]() 在坐标原点,顶点
在坐标原点,顶点![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() 为边
为边![]() 的中点,
的中点,![]() 是边
是边![]() 上的一个动点,当
上的一个动点,当![]() 的周长最小时,点
的周长最小时,点![]() 的坐标为_________.
的坐标为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com