
【题目】阅读材料,回答问题:
两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个代数式互为有理化因式.例如:因为![]() ,
,![]() ,所
,所![]() 与
与![]() ,
,![]() 与
与![]() 互为有理化因式.
互为有理化因式.
(1)![]() 的有理化因式是 ;
的有理化因式是 ;
(2)这样,化简一个分母含有二次根式的式子时,采用分子、分母同乘以分母的有理化因式的方法就可以了,例如:
![]() ,
,

用上述方法对![]() 进行分母有理化.
进行分母有理化.
(3)利用所需知识判断:若![]() ,
,![]() ,则
,则![]() 的关系是 .
的关系是 .
(4)直接写结果:![]() .
.
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)如图;![]() 为线段
为线段![]() 上任意一点,将线段
上任意一点,将线段![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 得到线段DF,连结CF,过点
得到线段DF,连结CF,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() .
.
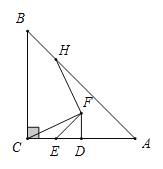
①若![]() ,求
,求![]() 的度数;
的度数;
②判断![]() 与
与![]() 的数量关系并加以证明.
的数量关系并加以证明.
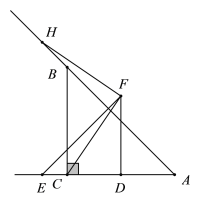
(2)如图,若![]() 为线段
为线段![]() 的延长线上任意一点,(1)中的其他条件不变,你在(1)②中得出的结论是否发生改变,给出证明.
的延长线上任意一点,(1)中的其他条件不变,你在(1)②中得出的结论是否发生改变,给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
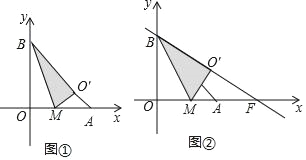
【题目】将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(2,0),点B(0,2),点O(0,0).点M为边OA上的一个动点(点M不与点O、A重合),沿着BM折叠该纸片,得顶点O的对应点O′.
(I)如图①,当点O′在边AB上时,求点O′的坐标;
(II)设直线BO′与x轴相交于点F.
①如图②,当BA平分∠MBF时,求点F的坐标;
②当OM=![]() 时,求点F的坐标(直接写出结果即可)
时,求点F的坐标(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两实根,实数
的两实根,实数![]() 、
、![]() 、
、![]() 、
、![]() 的大小关系可能是( )
的大小关系可能是( )
A. α<a<b<β B. a<α<β<b C. a<α<b<β D. α<a<β<b
查看答案和解析>>
科目:初中数学 来源: 题型:
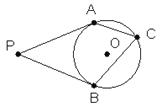
【题目】如图, PA、PB是⊙O的切线,切点为A、B,C是⊙O上一点(P与A、B不重合),若∠P=52°,则∠ACB=______________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组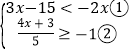
请结合题意填空,完成本题的解答.
(1)解不等式①,得________;
(2)解不等式②,得________;
(3)把不等式①和②的解集在数轴上表示出来;
![]()
(4)原不等式组的解集为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com