
【题目】如图,在![]() 中,
中,![]() , 点
, 点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,以
,以![]() 为边作等边
为边作等边![]() .
.
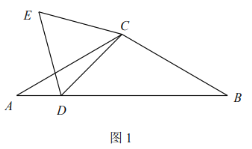
![]() 如图1,若
如图1,若![]() 求等边
求等边![]() 的边长;
的边长;
![]() 如图2,点
如图2,点![]() 在
在![]() 边上移动过程中,连接
边上移动过程中,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
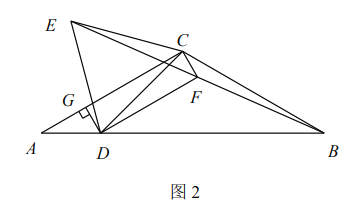
①求证:![]() ;
;
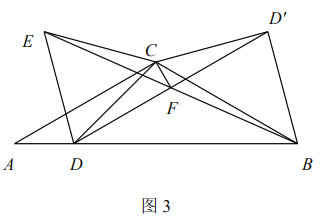
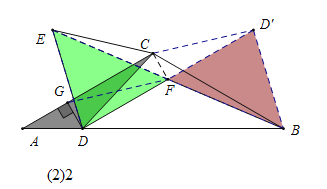
②如图3,将![]() 沿
沿![]() 翻折得
翻折得![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)证明见解析;(3)最小值为
;(2)证明见解析;(3)最小值为![]()
【解析】
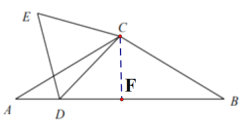
(1)过C做CF⊥AB,垂足为F,由题意可得∠B=30°,用正切函数可求CF的长,再用正弦函数即可求解;
(2) 如图(2)1:延长BC到G使CG=BC,易得△CGE≌△CAD,可得CF∥GE,得∠CFA=90°,CF=![]() GE再证DG=
GE再证DG=![]() AD,得CF=DG,可得四边形DGFC是矩形即可;
AD,得CF=DG,可得四边形DGFC是矩形即可;
(3)如图(2)2:设ED与AC相交于G,连接FG,先证△EDF≌△F D'B得BD'=DE,当DE最大时![]() 最小,然后求解即可;
最小,然后求解即可;
解:(1)如图:过C做CF⊥AB,垂足为F,
∵![]() ,
,![]()
∴∠A=∠B=30°,BF=3
∵tan∠B=![]()
∴CF=![]()
又∵sin∠CDB= sin45°=![]()
∴DC=![]()
∴等边![]() 的边长为
的边长为![]() ;
;
![]() ①如图(2)1:延长BC到G使CG=BC
①如图(2)1:延长BC到G使CG=BC

∵∠ACB=120°
∴∠GCE=180°-120°=60°,∠A=∠B=30°
又∵∠ACB=60°
∴∠GCE=∠ ACD
又∵CE=CD
∴△CGE≌△CAD(SAS)
∴∠G=∠ A=30°,GE=AD
又∵EF=FB
∴GE∥FC, GE=![]() FC,
FC,
∴∠BCF=∠G=30°
∴∠ACF=∠ACB-∠BCF=90°
∴CF∥DG
∵∠ A=30°
∴GD=![]() AD,
AD,
∴CF=DG
∴四边形DGFC是平行四边形,
又∵∠ACF=90°
∴四边形DGFC是矩形,
∴![]()
②)如图(2)2:设ED与AC相交于G,连接FG
由题意得:EF=BF, ∠EFD=∠D'FB ![]()
∴△EDF≌△F D'B
∴BD'=DE
∴BD'=CD
∴当BD'取最小值时,![]() 有最小值
有最小值
当CD⊥AB时,BD'min=![]() AC,
AC,
设CDmin=a,则AC=BC=2a,AB=2![]() a
a
![]() 的最小值为
的最小值为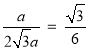 ;
;


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
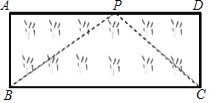
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
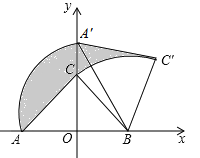
【题目】如图,![]() 中,
中,![]() ,
,![]() ,在以
,在以![]() 的中点
的中点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴建立的平面直角坐标系中,将
轴建立的平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 旋转至
旋转至![]() 轴的正半轴上的点
轴的正半轴上的点![]() 处,若
处,若![]() ,则图中阴影部分面积为________.
,则图中阴影部分面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O为BC边上一点,⊙O经过A、B两点,与BC边交于点E,点F为BE下方半圆弧上一点,FE⊥AC,垂足为D,∠BEF=2∠F.
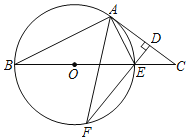
(1)求证:AC为⊙O切线.
(2)若AB=5,DF=4,求⊙O半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .动点
.动点![]() 以每秒
以每秒![]() 个单位的速度从点
个单位的速度从点![]() 开始向点
开始向点![]() 移动,直线
移动,直线![]() 从与
从与![]() 重合的位置开始,以相同的速度沿
重合的位置开始,以相同的速度沿![]() 方向平行移动,且分别与
方向平行移动,且分别与![]() 边交于
边交于![]() 两点,点
两点,点![]() 与直线
与直线![]() 同时出发,设运动的时间为
同时出发,设运动的时间为![]() 秒,当点
秒,当点![]() 移动到与点
移动到与点![]() 重合时,点
重合时,点![]() 和直线
和直线![]() 同时停止运动.在移动过程中,将
同时停止运动.在移动过程中,将![]() 绕点
绕点![]() 逆时针旋转,使得点
逆时针旋转,使得点![]() 的对应点
的对应点![]() 落在直线
落在直线![]() 上,点
上,点![]() 的对应点记为点
的对应点记为点![]() ,连接
,连接![]() ,当
,当![]() 时,
时,![]() 的值为___________.
的值为___________.
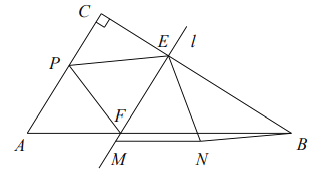
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=x2﹣2x+k的部分图象如图所示,则关于x的一元二次方程x2﹣2x+k=0的解一个为x1=3,则方程x2﹣2x+k=0另一个解x2=_____.
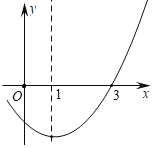
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明本学期4次数学考试成绩如下表如示:
成绩类别 | 第一次月考 | 第二次月考 | 期中 | 期末 |
成绩分 | 138 | 142 | 140 | 138 |
(1)小明4次考试成绩的中位数为__________分,众数为______________分;
(2)学校规定:两次月考的平均成绩作为平时成绩,求小明本学期的平时成绩;
(3)如果本学期的总评成绩按照平时成绩占20%、期中成绩占30%、期末成绩占50%计算,那么小明本学期的数学总评成绩是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA1=2,∠A1Ox=30°,以OA1为直角边作Rt△OA1A2,并使∠A1OA2=60°,再以A1A2为直角边作Rt△A1A2A3,并使∠A2A1A3=60°,再以A2A3为直角边作Rt△A2A3A4,并使∠A3A2A4=60°,…,按此规律进行下去,则A2020的坐标是_____.
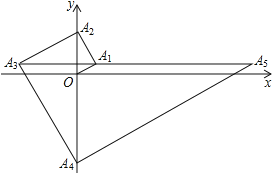
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com