
【题目】(1)尺规作图:如图,![]() 、
、![]() 是平面上两个定点,在平面上找一点
是平面上两个定点,在平面上找一点![]() ,使
,使![]() 构成等腰直角三角形,且
构成等腰直角三角形,且![]() 为直角顶点.(画出一个点
为直角顶点.(画出一个点![]() 即可)
即可)

(2)在(1)的条件下,若![]() ,
,![]() ,则点
,则点![]() 的坐标是________.
的坐标是________.
【答案】(1)见解析(2)![]()
【解析】
(1)如图作线段AB的垂直平分线MN交AB于点O,以O为圆心,OA为半径作⊙O交直线MN于C,C′,连接AC,BC,AC′BC′,点C或C′即为所求;
(2)如图,由勾股定理求出AB的长,再证明△NAE∽△BAO,求出AN,EN的长,再证明△NCD∽△NBE,求出CD,OD的长,进行可求点C的坐标,同理可求点![]() 的坐标.
的坐标.
(1)如图作线段AB的垂直平分线MN交AB于点O,以O为圆心,OA为半径作⊙O交直线MN于C,C′,连接AC,BC,AC′BC′,点C或C′即为所求.

(2)建立平面直角坐标系如图,CD⊥AN,EG⊥OB,![]() ,EG⊥OB,垂足分别为D,F,G.
,EG⊥OB,垂足分别为D,F,G.
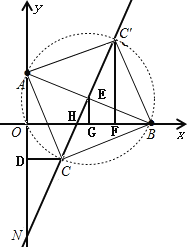
∵A(0,2),B(4,0),
∴OA=2,OB=4,
∴AB=![]()
∵E是圆心,AB是直径,
∴AE=![]() AB=
AB=![]() ,CE=
,CE=![]()
在△AOB和△AEN中,
∵∠NAE=∠BAO,∠AEN=∠AOB,
∴△AOB∽△AEN
∴![]()
∴NE=![]() ,CN=
,CN=![]() ,
,
∴AN=![]()
同理可证,△NCD∽△NAE,
∴![]() ,
,
∴![]() ,
,
∴CD=1,ND=2,
∴OD=5-2-2=1,
∴点C的坐标为(1,-1);
∵AO=2,
∴EG=1,
易证△EGH∽△NOH,
∴![]() ,即
,即![]()
∴![]() ,
,
∴HG=![]() ,OH=
,OH=![]()
∵ ![]() ,EG⊥OB,
,EG⊥OB,
∴△EHG∽△![]() ,
,
∴![]() ,即
,即 ,
,
∴![]() ,
,![]()
∴GF=1,
∴OF=2+1=3,
∴点![]() 的坐标为(3,3).
的坐标为(3,3).


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,以O为圆心,OA为半径的圆与BC相切与点B,与OC相交于点D.
中,以O为圆心,OA为半径的圆与BC相切与点B,与OC相交于点D.

(1)求![]() 的度数.
的度数.
(2)如图,点E在⊙O上,连接CE与⊙O交于点F,若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边AD、AB的长分别为3、8,边BC落在x轴上,E是DC的中点,连接AE.
(1)若点B坐标为(﹣6,0),求直线AE的表达式;
(2)反比例函数y=![]() (x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;
(x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;
(3)在(2)的条件下,连接矩形ABCD两对边AD与BC的中点M、N,设线段MN与反比例函数图象交于点P,将线段MN沿x轴向右平移n个单位,若MP<NP,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E是BC上的一点,F在线段DE上,且∠AFE=∠ADC.
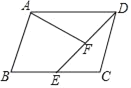
(1)若∠AFE=70°,∠DEC=40°,求∠DAF的大小;
(2)若DE=AD,求证:△AFD≌△DCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,∠A=30°,BD是⊙O的切线,C为切点,AB与⊙O相交于点E,OC=CD,BC=2,OD与⊙O相交于点F,则弧EF的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出了A,B两种上宽带网的收费方式(详情见下表)
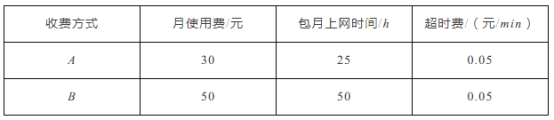
设月上网时间为x h(x为非负整数),请根据表中提供的信息回答下列问题
(1)设方案A的收费金额为y1元,方案B的收费金额为y2元,分别写出y1,y2关于x的函数关系式;
(2)当35<x<50时,选取哪种方式能节省上网费,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,点M是AC边的中点,点N是BC边上的任意一点,若点C关于直线MN的对称点C′恰好落在△ABC的中位线上,则CN的长为_____.
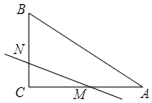
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com