
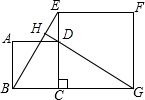
 (2012•内江模拟)如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG,并延长交GD于H.试猜想线段BE和DG的数量及位置关系,并证明你的猜想.
(2012•内江模拟)如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG,并延长交GD于H.试猜想线段BE和DG的数量及位置关系,并证明你的猜想. ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
|


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
(2012•内江模拟)为了解某班学生每天使用零花钱的情况,小敏随机调查了15名同学,结果如下表:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•内江模拟)如图,直角梯形纸片ABCD,AD⊥AB,AD=CD=4,点E、F分别在线段AB、CD上,将△AEF沿EF翻折,点A落在线段CD上的点P处,若AE=5,则PF的长为( )
(2012•内江模拟)如图,直角梯形纸片ABCD,AD⊥AB,AD=CD=4,点E、F分别在线段AB、CD上,将△AEF沿EF翻折,点A落在线段CD上的点P处,若AE=5,则PF的长为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com