(1)
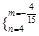
(2)y=
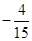
(x-4)
2+
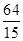
(3) (3,0),(4,0)解析:
(1)由
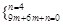
---------1分,得
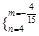
---------2分
(2) ∵四边形ABCD为菱形,AB=5 ∴AD=5---------1分
∴y=m(x+1-5)
2+n-m =
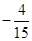
(x-4)
2+
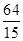
---------2分
(3) ∵C(8,0) ∴直线AC解析式为y=
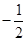
x+4 ∴E(4,2),CE=
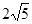
---------1分
∵AC=
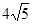
∴AE
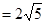
∵以点C、E、F为顶点的三角形与△ABE相似
∴F不在BC延长线上,故F在C的左侧- -1分

ⅰ

时,
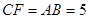
∴F(3,0) ---------1分
ⅱ

时
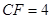
∴F(4,0) ---------1分 ∴F(4,0)或(3,0)
(1)已知了抛物线图象上A、B两点的坐标,将它们代入抛物线的解析式中,即可求得m、n的值.
(2)根据A、B的坐标,易求得AB的长;根据平移的性质知:四边形一定为平行四边形,若四边形为菱形,那么必须满足AB=AD,由此可确定平移的距离,根据“左加右减”的平移规律即可求得平移后的抛物线解析式.
(3)易求得直线AC的解析式,联立平移后的抛物线对称轴,可得到
E点的坐标,进而可求
EC、AE的长;所以以点C、E、F为顶点的三角形与△ABE相似,可分两种情况考虑:①

,②

,根据上述两种不同的相似三角形所得不同的比例线段,即可求得不同的CF长,进而可求得F点的坐标

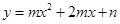 上.
上.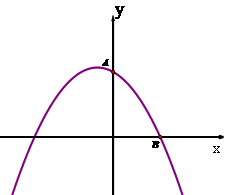
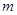 、n;
、n;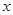 轴上找点F,使得以点C、E、F为顶点的三角形与△ ABE相似。
轴上找点F,使得以点C、E、F为顶点的三角形与△ ABE相似。 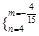 (2)y=
(2)y=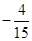 (x-4)2+
(x-4)2+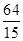 (3) (3,0),(4,0)解析:
(3) (3,0),(4,0)解析: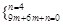 ---------1分,得
---------1分,得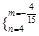 ---------2分
---------2分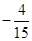 (x-4)2+
(x-4)2+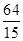 ---------2分
---------2分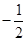 x+4 ∴E(4,2),CE=
x+4 ∴E(4,2),CE=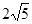 ---------1分
---------1分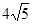 ∴AE
∴AE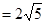

 时,
时,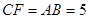 ∴F(3,0) ---------1分
∴F(3,0) ---------1分 时
时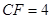 ∴F(4,0) ---------1分 ∴F(4,0)或(3,0)
∴F(4,0) ---------1分 ∴F(4,0)或(3,0) ,②
,② ,根据上述两种不同的相似三角形所得不同的比例线段,即可求得不同的CF长,进而可求得F点的坐标
,根据上述两种不同的相似三角形所得不同的比例线段,即可求得不同的CF长,进而可求得F点的坐标 

 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( ) 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设