
 ×360°=60°,得到△OAB为等边三角形,根据等边三角形的性质即可求得弦AB,弦心距;
×360°=60°,得到△OAB为等边三角形,根据等边三角形的性质即可求得弦AB,弦心距;
 ×360°=60°,
×360°=60°, AB=2
AB=2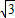 ,
,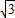 .
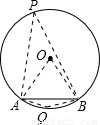
.
 AOB=30°,
AOB=30°, ;30°或150°.
;30°或150°.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012年北师大版初中数学九年级下3.2圆的对称性练习卷(解析版) 题型:填空题
圆的一条弦把圆分为5: 1 两部分, 如果圆的半径是2cm, 则这条弦的长是_____cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com