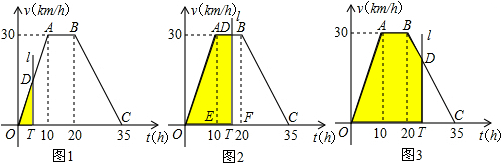
解:设直线l交v与t的函数图象于D点,
(1)由图象知,点A的坐标为(10,30),
故直线OA的解析式为v=3t,
当t=4时,D点坐标为(4,12),
∴OT=4,TD=12,
∴S=

×4×12=24(km);
(2)当0≤t≤10时,此时OT=t,TD=3t(如图1),
∴S=

•t•3t=

t
2,
当10<t≤20时,此时OT=t,AD=ET=t-10,TD=30(如图2),
∴S=S
△AOE+S
矩形ADTE=

×10×30+30(t-10)=30t-150,
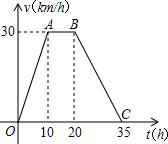
当20<t≤35时,∵B,C的坐标分别为(20,30),(35,0),
∴直线BC的解析式为v=-2t+70,
∴D点坐标为(t,-2t+70),
∴TC=35-t,TD=-2t+70(如图3),
∴S=S
梯形OABC-S
△DCT=

(10+35)×30-

(35-t)(-2t+70)=-(35-t)
2+675;
(3)S
1=
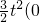
≤t≤10)最大值为150≤650,
S
2=30t-150=650,
t=
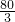
>20不可能,
当t=35时,S=-(35-35)
2+675=675(km),而450<650<675,
所以青白江城会受到影响,且影响时间t应在20h至35h之间,
由-(35-t)
2+675=650,解得t=30或t=40(不合题意,舍去).
所以在雷雨云发生后30h它将侵袭到青白江城.
分析:(1)设直线l交v与t的函数图象于D点.由图象知,点A的坐标为(10,30),故直线OA的解析式为v=3t,
当t=4时,D点坐标为(4,12)进而得出即可;
(2)分类讨论:当0≤t≤10时;当10<t≤20时;当20<t≤35时;
(3)根据t的值对应求S,然后根据青白江距M地650km分别解答.
点评:本题考查的是二次函数与一次函数在实际生活中的运用,比较复杂,解答此题的关键是根据图形反映的数据进行分段计算,难度适中.

 解:设直线l交v与t的函数图象于D点,
解:设直线l交v与t的函数图象于D点, ×4×12=24(km);
×4×12=24(km); •t•3t=
•t•3t= t2,
t2, ×10×30+30(t-10)=30t-150,
×10×30+30(t-10)=30t-150, (10+35)×30-
(10+35)×30- (35-t)(-2t+70)=-(35-t)2+675;
(35-t)(-2t+70)=-(35-t)2+675;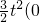 ≤t≤10)最大值为150≤650,
≤t≤10)最大值为150≤650,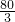 >20不可能,
>20不可能,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
