
【题目】某社区为了加强居民对新型冠状病毒肺炎防护知识的了解,鼓励社区居民在线参与作答《2020年新型冠状病毒肺炎的防护全国统一考试(全国卷)》试卷(满分100分),社区管理员随机从该社区抽取40名居民的答卷,并对他们的成绩(单位:分)进行整理、分析,过程如下:
收集数据
85 65 95 100 90 95 85 65 75 85 100 90 70 90 100 80 80 100 95 75 80 100 80 95 65 100 90 95 85 80 100 75 60 90 70 80 95 75 100 90
整理数据(每组数据可含最低值,不含最高值)
分组(分) | 频数 | 频率 |
60~70 | 4 | 0.1 |
70~80 | a | b |
80~90 | 10 | 0.25 |
90~100 | c | d |
100~110 | 8 | 0.2 |
分析数据
(1)填空:a= ,b= ,c= ,d= ;
(2)补全频率分布直方图;
(3)由此估计该社区居民在线答卷成绩在 (分)范围内的人数最多;
(4)如果该社区共有800人参与答卷,那么可估计该社区成绩在90分及以上约为 人.
【答案】(1)6,0.15,12,0.3;(2)见解析;(3):90~100;(4)400
【解析】
(1)根据数据找出a,c再求出相应的b,d.
(2)根据(1)画图即可.
(3)从直方图中直接找出频率最高者即为所求.
(4)总数乘以频率即可.
解:(1)由题意可知:
第二组的频数a=6,第四组的频数c=12,
∴第二组的频率为:6÷40=0.15,第四组的频率为:12÷40=0.3.
故答案为:6,0.15,12,0.3;
(2)如下图即为补全的频率分布直方图;
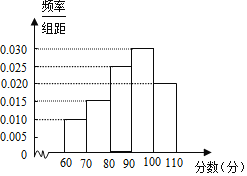
(3)由此估计该社区居民在线答卷成绩在90~100(分)范围内的人数最多.
故答案为:90~100;
(4)800×(0.3+0.2)=400(人).
答:如果该社区共有800人参与答卷,那么可估计该社区成绩在90分及以上约为400人.
故答案为:400.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点D、E分别是边BC、AB上一点,DE∥AC,BD=5![]() ,把△BDE绕着点B旋转得到△BD'E'(点D、E分别与点D',E'对应),如果点A,D'、E'在同一直线上,那么AE'的长为_____.
,把△BDE绕着点B旋转得到△BD'E'(点D、E分别与点D',E'对应),如果点A,D'、E'在同一直线上,那么AE'的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
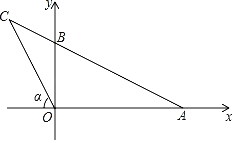
【题目】如图,在平面直角坐标系中,AB=3![]() ,连结AB并延长至C,连结OC,若满足OC2=BCAC,tanα=2,则点C的坐标为( )
,连结AB并延长至C,连结OC,若满足OC2=BCAC,tanα=2,则点C的坐标为( )
A.(﹣2,4)B.(﹣3,6)C.(﹣![]() ,
,![]() )D.(﹣
)D.(﹣![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过A(-1,0)、B(3,0),直线AD交抛物线于点D,点D的横坐标为2,点P(m,n)是线段AD上的动点.
过A(-1,0)、B(3,0),直线AD交抛物线于点D,点D的横坐标为2,点P(m,n)是线段AD上的动点.
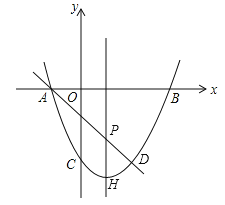
(1)求抛物线和直线AD的解析式;
(2)过点P的直线垂直于x轴,交抛物线于点H,
①求线段PH的长度l与m的关系式;
②当PH=2时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中(如图),已知经过点A(﹣3,0)的抛物线y=ax2+2ax﹣3与y轴交于点C,点B与点A关于该抛物线的对称轴对称,D为该抛物线的顶点.
(1)直接写出该抛物线的对称轴以及点B的坐标、点C的坐标、点D的坐标;
(2)联结AD、DC、CB,求四边形ABCD的面积;
(3)联结AC.如果点E在该抛物线上,过点E作x轴的垂线,垂足为H,线段EH交线段AC于点F.当EF=2FH时,求点E的坐标.
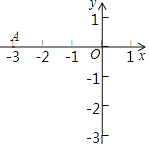
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组开展了一次课外活动,过程如下:如图1,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.
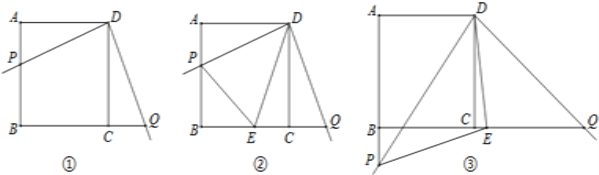
(1)求证:DP=DQ;
(2)如图2,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)如图3,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B,与y轴分别交于点C,其中点A(﹣1,0),OB=4OA,OC=2OA
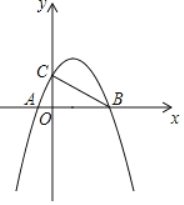
(1)求抛物线的解析式.
(2)点P是线段AB一动点,过P作PD∥AC交BC于D,当△PCD面积最大时,求点P的坐标.
(3)点M是位于线段BC上方的抛物线上一点,当∠ABC恰好等于△BCM中的某个角时,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
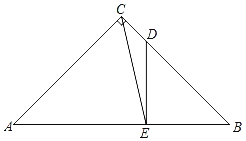
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D在边BC上,且BD=3CD,DE⊥AB,垂足为点E,联结CE.
(1)求线段AE的长;
(2)求∠ACE的余切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com