
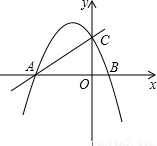
 如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-
如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=- 时,y取最大值
时,y取最大值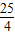 .
. x+a与(1)中所求的抛物线交于点M、N,两点,问:
x+a与(1)中所求的抛物线交于点M、N,两点,问: )
) 时,y取最大值
时,y取最大值 ,得到抛物线的顶点坐标为(-
,得到抛物线的顶点坐标为(- ,
,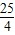 ),可写出抛物线的顶点式,再根据抛物线的解析式求出A、C的坐标,然后将A、C的坐标代入
),可写出抛物线的顶点式,再根据抛物线的解析式求出A、C的坐标,然后将A、C的坐标代入 x+a与抛物线y=-x2-x+6的交点为M(xM,yM),N(xN,yN)(M在N左侧),则xM、xN是方程x2+
x+a与抛物线y=-x2-x+6的交点为M(xM,yM),N(xN,yN)(M在N左侧),则xM、xN是方程x2+ x+a-6=0的两个根,由一元二次方程根与系数关系得,xM+xN=-
x+a-6=0的两个根,由一元二次方程根与系数关系得,xM+xN=- ,xM•xN=a-6,进而求出yM•yN=
,xM•xN=a-6,进而求出yM•yN= (a-6)-
(a-6)- a+a2.
a+a2. 时,y取最大值
时,y取最大值 ,
, )2+
)2+ ,即y=-x2-x+6;
,即y=-x2-x+6;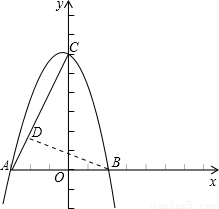 即A点坐标是(-3,0),B点坐标是(2,0).
即A点坐标是(-3,0),B点坐标是(2,0). ,
, ,
, =
= ,
, ∴AP:PC=1:3,
∴AP:PC=1:3,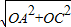 =3
=3 .
.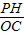 =
=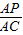 =
= ,
, ,
, =2x+6,
=2x+6, ,
, ,
, );
); 当点P在CA延长线时,作PG⊥x轴,点G为垂足.
当点P在CA延长线时,作PG⊥x轴,点G为垂足. =
= =
= ,
, ,
, ,-3).
,-3). ,
, )或(-
)或(- ,-3).
,-3). x+a与抛物线y=-x2-x+6的交点为M(xM,yM),N(xN,yN)(M在N左侧).
x+a与抛物线y=-x2-x+6的交点为M(xM,yM),N(xN,yN)(M在N左侧). ,
, 为方程组
为方程组 的解,
的解, x+a-6=0,
x+a-6=0, x+a-6=0的两个根,
x+a-6=0的两个根, ,xM•xN=a-6,
,xM•xN=a-6, xM+a)(
xM+a)( xN+a)=
xN+a)= xM•xN+
xM•xN+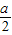 (xM+xN)+a2=
(xM+xN)+a2= (a-6)-
(a-6)- a+a2.
a+a2. ①存在a的值,使得∠MON=90°.理由如下:
①存在a的值,使得∠MON=90°.理由如下: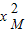 +
+ +
+ +
+ =(xM-xN)2+(yM-yN)2,
=(xM-xN)2+(yM-yN)2, (a-6)-
(a-6)- a+a2=0,
a+a2=0, ,
, ;
; +
+ +
+ +
+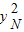 <(xM-xN)2+(yM-yN)2,
<(xM-xN)2+(yM-yN)2, (a-6)-
(a-6)- a+a2<0,
a+a2<0, ,
, .
.

科目:初中数学 来源: 题型:
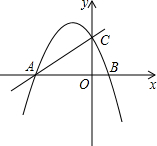 (2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-
(2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-| 1 |
| 2 |
| 25 |
| 4 |
| 1 |
| 2 |
| (x2-x1)2+(y2-y1)2 |
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(湖北黄石卷)数学(带解析) 题型:解答题
如图1所示,已知直线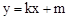 与x轴、y轴分别交于A、C两点,抛物线
与x轴、y轴分别交于A、C两点,抛物线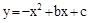 经过A、C两点,点B是抛物线与x轴的另一个交点,当
经过A、C两点,点B是抛物线与x轴的另一个交点,当 时,y取最大值
时,y取最大值 .
.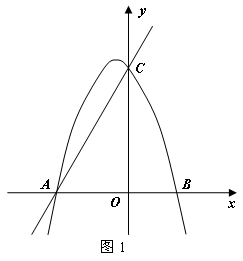
(1)求抛物线和直线的解析式;
(2)设点P是直线AC上一点,且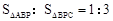 ,求点P的坐标;
,求点P的坐标;
(3)若直线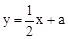 与(1)中所求的抛物线交于M、N两点,问:
与(1)中所求的抛物线交于M、N两点,问:
①是否存在a的值,使得∠MON=900?若存在,求出a的值;若不存在,请说明理由;
②猜想当∠MON>900时,a的取值范围(不写过程,直接写结论).
(参考公式:在平面直角坐标系中,若M(x1,y1),N(x2,y2),则M,N两点间的距离为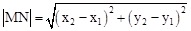 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com