练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在四边形中，，要使四边形是平行四边形，下列可添加的条件不正确的是（ ）

    A.B.C.D.

    【答案】D

    【解析】

    平行四边形的五种判定方法分别是:两组对边分别平行的四边形是平行四边形；两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形．根据平行四边形的判定,逐个验证即可．

    解：A.∵，

    ∴四边形是平行四边形（一组对边平行且相等的四边形是平行四边形），故本选项不符合题意；

    B.∵，

    ∴四边形是平行四边形（两组对边分别平行的四边形是平行四边形），故本选项不符合题意；

    C.∵

    ∴

    ∵

    ∴

    ∴

    ∴四边形是平行四边形（两组对边分别平行的四边形是平行四边形），故本选项不符合题意；

    D.若添加不一定是平行四边形，如图：

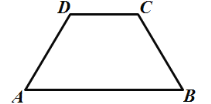
    四边形ABCD为等腰梯形，故本选项符合题意．

    故选：D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，∠MON=30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4…均为等边三角形．若OA1=1，则△AnBnAn+1的边长为______．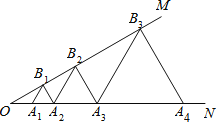

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某种油菜籽在相同条件下的发芽实验结果如下表：

    每批粒数n

    100

    150

    200

    500

    800

    1 000

    发芽的粒数m

    65

    111

    136

    345

    560

    700

    发芽的频率

    0.65

    0.74

    0.68

    0.69

    a

    b

    （1）a＝ ，b＝ ；

    （2）这种油菜籽发芽的概率估计值是多少？请简要说明理由；

    （3）如果该种油菜籽发芽后的成秧率为90%，则在相同条件下用10 000粒该种油菜籽可得到油菜秧苗多少棵？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】式子的计算结果的个位数上的数字（ ）

    A.1B.3C.7D.9

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD，AB=6，点E在边CD上，CE=2DE，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF，下列结论：①△ABG≌△AFG；②BG=GC；③EG=DE+BG；④AG∥CF；⑤S△FCA=3.6，其中正确结论是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,将直角三角形ABC沿AB方向平移得到直角三角形DEF,已知BE=3,BE=3,FG=1,AC=5,则图中阴影部分的面积为（ ）

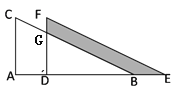
    A.10B.13.5C.20D.9.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某办公楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，办公楼在建筑物的墙上留下高3米的影子CE，而当光线与地面夹角是45°时，办公楼顶A在地面上的影子F与墙角C有27米的距离（B，F，C在一条直线上）．

    （1）求办公楼AB的高度；

    （2）若要在A，E之间挂一些彩旗，请你求出A，E之间的距离．

    （参考数据：sin22°≈，cos22°≈，tan22°≈）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+1经过点（2，6），且与直线y=x+1相交于A，B两点，点A在y轴上，过点B作BC⊥x轴，垂足为点C（4，0）．

    （1）求抛物线的解析式；

    （2）若P是直线AB上方该抛物线上的一个动点，过点P作PD⊥x轴于点D，交AB于点E，求线段PE的最大值；

    （3）在（2）的条件，设PC与AB相交于点Q，当线段PC与BE相互平分时，请求出点Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：

    材料1：对于一个关于的二次三项式，除了可以利用配方法求请多项式的取值范围外，爱思考的小川同学还想到了其他的方法：比如先令，然后移项可得：，再利用一元二次方程根的判别式来确定的取值范围，请仔细阅读下面的例子：

    例：求的取值范围：

    解：令

    ∴

    ∴

    ∴

    ∴；

    材料2：在学习完一元二次方程的解法后，爱思考的小川同学又想到仿造一元二次方程的解法来解决一元二次不等式的解集问题，他的具体做法如下：

    若关于的一元二次方程（）有两个不相等的实数根，（）

    则关于的一元二次不等式（）的解集为：或．

    则关于的一元二次不等式（）的解集为：．

    请根据上述材料，解答下列问题：

    （1）若关于的二次三项式（为常数）的最小值为－6，则________；

    （2）求出代数式的取值范围；

    （3）若关于的代数式（其中、为常数，且）的最小值为－4，最大值为7，请求出满足条件的，的值．

    查看答案和解析>>

    同步练习册答案