
如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8㎝,BC=4㎝,AB=5㎝.从初始时刻开始,动点P沿着P、Q分别从点A,B同时出发,运动速度均为1㎝/s,动点P沿A—B—C—E的方向运动,到点E停止;动点Q沿B—C—E—D的方向运动,到点D停止,设运动时间为 s,△PAQ的面积为
s,△PAQ的面积为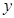 ㎝2.(这里我们把线段的面积看作是0)
㎝2.(这里我们把线段的面积看作是0)
解答下列问题
(1)当 =2s时,
=2s时,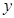 = ㎝2,当
= ㎝2,当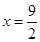 s时,
s时,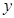 = ㎝2;
= ㎝2;
(2)当5≤ ≤14时,求
≤14时,求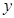 与
与 之间的函数关系式;
之间的函数关系式;
(3)当动点P在线段BC上运动时,求出
 梯形ABCD时
梯形ABCD时 的值;
的值;
(4)直接写出整个运动过程中,使PQ与四边形ABCE的对角线平行的所有 的值.
的值.
(1)2,9;(2)当5≤ ≤9时,
≤9时, ,当9<
,当9< ≤13时,
≤13时, ,当13<
,当13< ≤14时,
≤14时,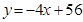 ;(3)
;(3) =7;(4)
=7;(4)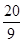 ,
,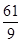 ,
,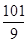 .
.
解析试题分析:(1)当x=2s时,AP=2,BQ=2,利用三角形的面积公式直接可以求出y的值,当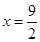 s时,三角形PAQ的高就是4,底为4.5,由三角形的面积公式可以求出其解.
s时,三角形PAQ的高就是4,底为4.5,由三角形的面积公式可以求出其解.
(2)当5≤ ≤14 时,求y与x之间的函数关系式.要分为三种不同的情况进行表示:当5≤
≤14 时,求y与x之间的函数关系式.要分为三种不同的情况进行表示:当5≤ ≤9时,当9<
≤9时,当9< ≤13时,当13<
≤13时,当13< ≤14时.
≤14时.
(3)可以由已知条件求出S梯形ABCD,然后根据条件求出y值,代入当5≤x≤9时的解析式就可以求出x的值.
(4)利用相似三角形的性质,相似三角形的对应线段成比例就可以求出对应的x的值.
(1)当x=2s时,AP=2,BQ=2
∴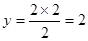
当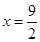 s时,AP=4.5,Q点在EC上
s时,AP=4.5,Q点在EC上
∴ ;
;
(2)当5≤ ≤9时
≤9时
y=S梯形ABCQ-S△ABP-S△PCQ=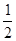 (5+x-4)×4-
(5+x-4)×4-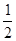 ×5(x-5)-
×5(x-5)-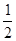 (9-x)(x-4)
(9-x)(x-4)
当9< ≤13时
≤13时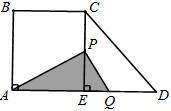
y=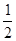 (x-9+4)(14-x)
(x-9+4)(14-x)
当13< ≤14时
≤14时
y=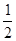 ×8(14-x)
×8(14-x)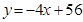 ;
;
(3)当动点P在线段BC上运动时
∵y=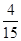 S梯形ABCD=
S梯形ABCD=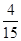 ×
×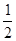 (4+8)×5=8
(4+8)×5=8
∴8=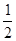 x2-7x+
x2-7x+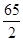 ,即x2-14x+49=0,解得:x1=x2=7
,即x2-14x+49=0,解得:x1=x2=7
∴当x=7时,y=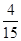 S梯形ABCD
S梯形ABCD
(4)设运动时间为x秒,
当PQ∥AC时,BP=5-x,BQ=x,
此时△BPQ∽△BAC,
故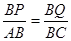 ,即
,即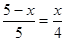 ,
,
解得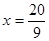 ;
;
当PQ∥BE时,PC=9-x,QC=x-4,
此时△PCQ∽△BCE,
故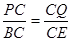 ,即
,即 ,
,
解得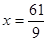 ;
;
当PQ∥BE时,EP=14-x,EQ=x-9,
此时△PEQ∽△BAE,
故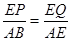 ,即
,即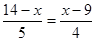 ,
,
解得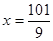 .
.
由题意得x的值为: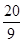 ,
,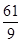 ,
,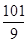 .
.
考点:二次函数的综合题
点评:二次函数的综合题是初中数学的重点和难点,在中考中极为常见,一般压轴题形式出现,难度较大.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,cosC=
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,cosC=
| ||
| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com