
【题目】如图,已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
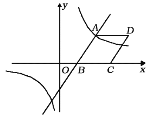
(1)填空:![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)以![]() 为边作菱形
为边作菱形![]() ,使点
,使点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在第一象限,求点
在第一象限,求点![]() 的坐标;
的坐标;
【答案】(1)3,12;(2)D的坐标为![]()
【解析】
(1)把点A(4,n)代入一次函数y=![]() x-3,得到n的值为3;再把点A(4,3)代入反比例函数
x-3,得到n的值为3;再把点A(4,3)代入反比例函数![]() ,得到k的值为12;
,得到k的值为12;
(2)根据坐标轴上点的坐标特征可得点B的坐标为(2,0),过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,根据勾股定理得到AB=![]() ,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标.
,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标.
(1)把点A(4,n)代入一次函数![]() ,可得
,可得![]() ;
;
把点A(4,3)代入反比例函数![]() ,可得
,可得![]() ,
,
解得k=12.
(2)∵一次函数![]() 与
与![]() 轴相交于点B,
轴相交于点B,
由![]() ,解得
,解得![]() ,
,
∴点B的坐标为(2,0)
如图,过点A作![]() 轴,垂足为E,
轴,垂足为E,
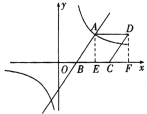
过点D作![]() 轴,垂足为F,
轴,垂足为F,
∵A(4,3),B(2,0)
∴OE=4,AE=3,OB=2,
∴ BE=OE-OB=4-2=2
在![]() 中,
中,![]() .
.
∵四边形ABCD是菱形,
∴![]() ,
,
∴![]() .
.
∵![]() 轴,
轴,![]() 轴,
轴,
∴![]() .
.
在![]() 与
与![]() 中,
中, ![]() ,
,![]() ,AB=CD,
,AB=CD,
∴![]() ,
,
∴CF=BE=2,DF=AE=3,
∴![]() .
.
∴点D的坐标为![]()


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形硬纸片ABCD的顶点A在![]() 轴的正半轴及原点上滑动,顶点B在
轴的正半轴及原点上滑动,顶点B在![]() 轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为12π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为
轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为12π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为![]() ,其中正确的结论是_________(填写序号).
,其中正确的结论是_________(填写序号).
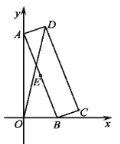
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天猫商城某网店销售某款蓝牙耳机,进价为100元![]() 在元旦即将来临之际,开展了市场调查,当蓝牙耳机销售单价是180元时,平均每月的销售量是200件,若销售单价每降低2元,平均每月就可以多售出10件.
在元旦即将来临之际,开展了市场调查,当蓝牙耳机销售单价是180元时,平均每月的销售量是200件,若销售单价每降低2元,平均每月就可以多售出10件.
![]() 设每件商品降价x元,该网店平均每月获得的利润为y元,请写出y与x元之间的函数关系;
设每件商品降价x元,该网店平均每月获得的利润为y元,请写出y与x元之间的函数关系;
![]() 该网店应该如何定价才能使得平均每月获得的利润最大,最大利润是多少元?
该网店应该如何定价才能使得平均每月获得的利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把菱形![]() 向右平移至
向右平移至![]() 的位置,作
的位置,作![]() ,垂足为
,垂足为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() :④
:④![]() .
.
则其中所有成立的结论是( )
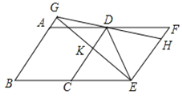
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是_____.
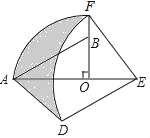
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日,深圳高级中学(集团)南北校区初三学生参加东校区下午![]() 时的交流活动,南校区学生中午
时的交流活动,南校区学生中午![]() 乘坐校车出发,沿正北方向行12公里到达北校区,然后南北校区一同前往东校区(等待时间不计).如图所示,已知东校区在南校区北偏东
乘坐校车出发,沿正北方向行12公里到达北校区,然后南北校区一同前往东校区(等待时间不计).如图所示,已知东校区在南校区北偏东![]() 方向,在北校区北偏东
方向,在北校区北偏东![]() 方向.校车行驶状态的平均速度为
方向.校车行驶状态的平均速度为![]() ,途中一共经过30个红绿灯,平均每个红绿灯等待时间为30秒.
,途中一共经过30个红绿灯,平均每个红绿灯等待时间为30秒.
(1)求北校区到东校区![]() 的距离;
的距离;
(2)通过计算,说明南北校区学生能否在![]() 前到达东校区.(本题参考数据:
前到达东校区.(本题参考数据:![]() ,
,![]() )
)
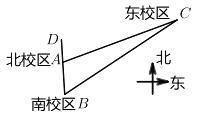
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+4的图象与反比例函数y2=![]() 的图象交于A(﹣1,a),B两点,与x轴交于点C.
的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求k.
(2)根据图象直接写出y1>y2时,x的取值范围.
(3)若反比例函数y2=![]() 与一次函数y1=x+4的图象总有交点,求k的取值.
与一次函数y1=x+4的图象总有交点,求k的取值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() .
.

(1)求二次函数![]() 的表达式;
的表达式;
(2)过点![]() 作
作![]() 平行于
平行于![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 为抛物线上的一点(点
为抛物线上的一点(点![]() 在
在![]() 上方),作
上方),作![]() 平行于
平行于![]() 轴交
轴交![]() 于点
于点![]() ,当点
,当点![]() 在何位置时,四边形
在何位置时,四边形![]() 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com