解:(1)猜想得:EF=
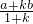
,
证明:过点E作BC的平行线交AB于G,交CD的延长线于H.
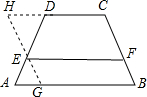
∵AB∥CD,
∴△AGE∽△DHE,
∴
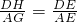
,
又∵EF∥AB∥CD,
∴CH=EF=GB,
∴DH=EF-a,AG=b-EF,
∴
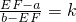
,可得
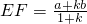
;
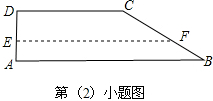
(2)在AD上取一点E,作EF∥AB交BC于点F,
设
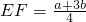
,
则EF=
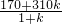
,
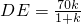
,
若S
梯形DCFE=S
梯形ABFE,则S
梯形ABCD=2S
梯形DCFE,
∵梯形ABCD、DCFE为直角梯形,
∴
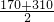
×70=2×

×(170+
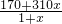
)×
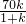
,
化简得12k
2-7k-12=0解得:
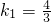
,
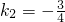
(舍去),
∴DE=
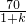
=30,
所以只需在AD上取点E,使DE=30米,作EF∥AB(或EF⊥DA),
即可将梯形分成两个直角梯形,且它们的面积相等.
分析:(1)本题可通过构建相似三角形来求解.过点E作BC的平行线交AB于G,交CD的延长线于H.那么四边形HCGB就是平行四边形,HC=BG=EF,因此HD=EF-a,AG=b-EF,那么可根据相似三角形HED和GEA得出的关于DH,AG,DE,AE的比例关系式,即可求出所求的比例关系式;
(2)可按照(1)的思路进行求解.在AD上取一点E,作EF∥AB交BC于点F,可先设DE:AE=k,那么可用k表示出DE和EF的长.由于被EF平分的两部分面积相等,因此梯形ABCD的面积=2×梯形DEFC的面积,由此可求出梯形DEFC的面积,然后根据DE,EF的长,表示出梯形DEFC的面积即可得出关于k的方程,经过解方程即可得出k的值,进而可确定具体的分割方案.
点评:本题考查了梯形中辅助线的常规作法以及相似三角形的判定等知识点.在梯形中通过作辅助线来构建平行四边形是常用的方法.

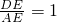 时,有
时,有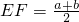 ;
;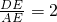 时,有
时,有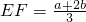 ;
;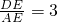 时,有
时,有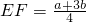 .
.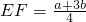 时,参照上述研究结论,请你猜想用k表示EF的一般结论,并给出证明;
时,参照上述研究结论,请你猜想用k表示EF的一般结论,并给出证明;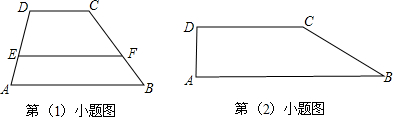
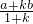 ,
,
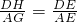 ,
,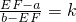 ,可得
,可得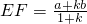 ;
;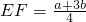 ,
,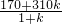 ,
,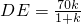 ,
,
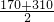 ×70=2×
×70=2× ×(170+
×(170+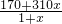 )×
)×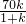 ,
,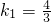 ,
,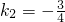 (舍去),
(舍去),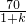 =30,
=30,

 CE、AF.
CE、AF.