
【题目】如图,在边长为 4 的等边△ABC 中,点 D 从点A 开始在射线 AB 上运动,速度为 1 个单位/秒,点F 同时从 C 出发,以相同的速度沿射线 BC 方向运动,过点D 作 DE⊥AC,连结 DF 交射线 AC 于点 G
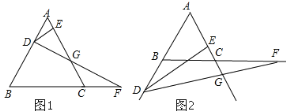
(1)当 DF⊥AB 时,求 t 的值;
(2)当点 D 在线段 AB 上运动时,是否始终有 DG=GF?若成立,请说明理由。
(3)聪明的斯扬同学通过测量发现,当点 D 在线段 AB 上时,EG 的长始终等于 AC 的一半,他想当点D 运动到图 2 的情况时,EG 的长是否发生变化?若改变,说明理由;若不变,求出 EG 的长。
【答案】(1)![]() ;(2)见详解;(3)不变.
;(2)见详解;(3)不变.
【解析】
(1)设AD=x,则BD=4-x,BF=4+x.当DF⊥AB时,通过解直角△BDF求得x的值,易得t的值;
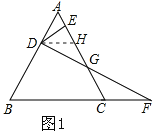
(2)如图1,过点D作DH∥BC交AC于点H,构建全等三角形:△DHG≌△FCG,结合全等三角形的对应边相等的性质和图中相关线段间的和差关系求得DG=GF;
(3)过F作FH⊥AC,可证△ADE≌△CFH,得DE=FH,AC=EH,再证△GDE≌△GFH,可得EG=GH,即可解题.
解:(1)设AD=x,则BD=4-x,BF=4+x.
当DF⊥AB时,∵∠B=60°,
∴∠DFB=30°,
∴BF=2BD,即4+x=2(4-x),
解得x=![]() ,
,
故t=![]() ;
;
(2)如图1,过点D作DH∥BC交AC于点H,则∠DHG=∠FCG.
∵△ABC是等边三角形,
∴△ADH是等边三角形,
∴AD=DH.
又AD=CF,
∴DH=FC.
∵在△DHG与△FCG中,
 ,
,
∴△DHG≌△FCG(AAS),
∴DG=GF;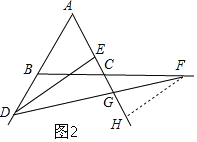
(3)如图2,过F作FH⊥AC,
在△ADE和△CFH中,
 ,
,
∴△ADE≌△CFH(AAS),
∴DE=FH,AE=CH,
∴AC=EH,
在△GDE和△GFH中,
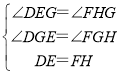 ∴△GDE≌△GFH(AAS),
∴△GDE≌△GFH(AAS),
∴EG=GH,
∴EG=![]() EH=
EH=![]() AC.
AC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】直线![]() 与
与![]() 轴、
轴、![]() 轴分別交于
轴分別交于![]() 、
、![]() 两点,
两点,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一点.
上一点.
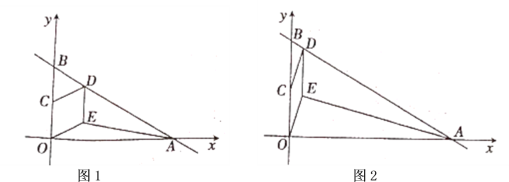
(1)求点![]() 、
、![]() 的坐标;
的坐标;
(2)若四边形![]() 是菱形,如图1,求
是菱形,如图1,求![]() 的面积;
的面积;
(3)若四边形![]() 是平行四边形,如图2,设点
是平行四边形,如图2,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定学生每天户外活动的平均时间不少于![]() 小时,小明为了解本班学生参加户外活动的情况,特进行了问卷调查.
小时,小明为了解本班学生参加户外活动的情况,特进行了问卷调查.
(1)在进行问卷调查时有如下步骤,按顺序排列为________(填序号).
①发问卷,让被调查人填写;②设计问卷;③对问卷的数据进行收集与整理;
④收回问卷;⑤得出结论.
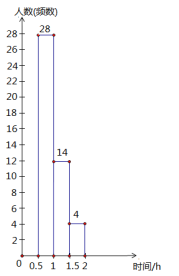
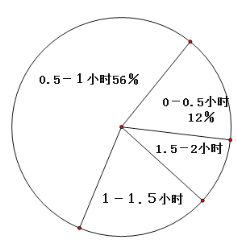
(2)小明根据调查结果,就本班学生每天参加户外活动的平均时间绘制了以下两幅不完整的统计图(图中![]() 表示大于等于
表示大于等于![]() 同时小于
同时小于![]() ,图中类似的记号均表示这一含义),请你根据图中提供的信息解答下列问题:
,图中类似的记号均表示这一含义),请你根据图中提供的信息解答下列问题:
①在这次调查中共调查了多少名学生?
②通过计算补全频数分布直方图;
③请你根据以上统计结果,就学生参加户外活动情况提出建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学解方程的过程,请仔细阅读,并解答所提出的问题.
![]()
解:去分母,得![]() ,①
,①
去括号,得![]() ,②
,②
移项,得![]() ,③
,③
合并同类项,得![]() ,④
,④
系数化为![]() ,得
,得![]() .⑤
.⑤
(1)聪明的你知道小明的解答过程在________(填序号)处出现了错误,出现错误的原因是违背了__________.
A.等式的基本性质![]() ;B.等式的基本性质
;B.等式的基本性质![]() ;C.去括号法则;D加法交换律.
;C.去括号法则;D加法交换律.
(2)请你写出正确的解答过程
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,点P从B出发,沿折线BE-ED-DC匀速运动,运动到点C停止.P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的函数关系图象如图②,则下列结论正确的有( )
①a=7 ②AB=8cm ③b=10 ④当t=10s时,y=12cm2 
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 是
是![]() 上的一动点(不与点
上的一动点(不与点![]() 重合),延长
重合),延长![]() 交射线
交射线![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 填空:①当
填空:①当![]() ________时,四边形
________时,四边形![]() 是矩形;②当
是矩形;②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在数轴上所对应的数分别是
在数轴上所对应的数分别是![]() ,其中
,其中![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)数轴上有一点![]() ,使得
,使得![]() ,求点
,求点![]() 所对应的数;
所对应的数;
(3)点![]() 为
为![]() 中点,
中点,![]() 为原点,数轴上有一动点
为原点,数轴上有一动点![]() ,求
,求![]() 的最小值及点
的最小值及点![]() 所对应的数的取值范围.
所对应的数的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com