
【题目】某超市销售一种饮料, 每瓶进价为![]() 元,当每瓶售价
元,当每瓶售价![]() 元时,日均销售量
元时,日均销售量![]() 瓶.经市场调查表明,每瓶售价每增加
瓶.经市场调查表明,每瓶售价每增加![]() 元,日均销售量减少
元,日均销售量减少![]() 瓶.
瓶.
(1)当每瓶售价为![]() 元时,日均销售量为 瓶;
元时,日均销售量为 瓶;
(2)当每瓶售价为多少元时,所得日均总利润为![]() 元;
元;
(3)当每瓶售价为多少元时,所得日均总利润最大?最大日均总利润为多少元?
【答案】(1)![]() ;(2)
;(2)![]() 元或
元或![]() 元;(3)
元;(3)![]() 元时利润最大,最大利润
元时利润最大,最大利润![]() 元
元
【解析】
(1)当每瓶售价为![]() 元时,每瓶售价增加1元,日均销售量减少80瓶,即可求解.
元时,每瓶售价增加1元,日均销售量减少80瓶,即可求解.
(2)设每瓶售价为x元,根据题意表示出每瓶利润,日销售量,根据等量关系列方程解答即可.
(3)设每瓶售价为a元,日均总利润为y元,求出y关于a的函数表达式,配方即可求解.
(1)当每瓶售价为![]() 元时,每瓶售价增加1元,日均销售量减少80瓶,560-80=480瓶
元时,每瓶售价增加1元,日均销售量减少80瓶,560-80=480瓶
故答案为:480
(2)设每瓶售价为x元时,所得日均总利润为![]() 元,根据题意得:
元,根据题意得:
![]()
解得:x1=12,x2=14
答:当每瓶的售价为12元或14元时,所得日均总利润为![]() 元.
元.
(3)设每瓶售价为a元,日均总利润为y元,根据题意得:
![]()
答:每瓶售价为13元时利润最大,最大利润1280元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
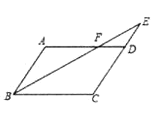
【题目】如图,在口ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= ![]() CD
CD
(1)求证:△ABF∽△CEB
(2)若△DEF的面积为2,求△CEB的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有![]() 个标号分别为
个标号分别为![]() 的小球,这些球除标号外无其它差别.从布袋里随机取出一个小球,记下标号为
的小球,这些球除标号外无其它差别.从布袋里随机取出一个小球,记下标号为![]() ,再从剩下的
,再从剩下的![]() 个小球中随机取出一个小球,记下标号为
个小球中随机取出一个小球,记下标号为![]() 记点
记点![]() 的坐标为
的坐标为![]() .
.
(1)请用画树形图或列表的方法写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)求两次取出的小球标号之和大于![]() 的概率;
的概率;
(3)求点![]() 落在直线
落在直线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣4x2﹣8mx﹣m2+2m的顶点p.
(1)点p的坐标为 (含m的式子表示)
(2)当﹣1≤x≤1时,y的最大值为5,则m的值为多少;
(3)若抛物线与x轴(不包括x轴上的点)所围成的封闭区域只含有1个整数点,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
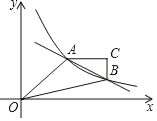
【题目】如图,在平面直角坐标系中,一次函数y=﹣![]() x+3的图象与反比例函数y=
x+3的图象与反比例函数y=![]() (x>0,k是常数)的图象交于A(a,2),B(4,b)两点.
(x>0,k是常数)的图象交于A(a,2),B(4,b)两点.
(1)求反比例函数的表达式;
(2)点C是第一象限内一点,连接AC,BC,使AC∥x轴,BC∥y轴,连接OA,OB.若点P在y轴上,且△OPA的面积与四边形OACB的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
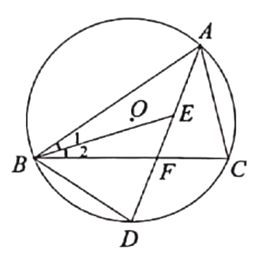
【题目】如图,△ABC内接于⊙O,∠ABC和 ∠BAC的平分线交于点E,延长AE分别交BC, ⊙O于点F, D,连接BD.
(1)求证: BD=DE.
(2)若BD=6,AD=10,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小芸设计的“过圆外一点作已知圆的切线”的尺规作图过程.
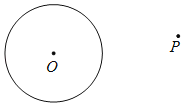
已知:⊙O及⊙O外一点P.
求作:⊙O的一条切线,使这条切线经过点P.
作法:①连接OP,作OP的垂直平分线l,交OP于点A;
②以A为圆心,AO为半径作圆,交⊙O于点M;
③作直线PM,则直线PM即为⊙O的切线.
根据小芸设计的尺规作图过程,
(1)用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成证明:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com