
【题目】2020年新冠肺炎疫情发生以来,我市广大在职党员积极参与社区防疫工作,助力社区坚决打赢疫情防控阻击战.其中,A社区有500名在职党员,为了解本社区2月—3月期间在职党员参加应急执勤的情况,A社区针对执勤的次数随机抽取50名在职党员进行调查,并对数据进行了整理、描述和分析,下面给出了部分信息.
次数x/次 | 频数 | 频率 |
0 ≤x< 10 | 8 | 0.16 |
10≤x< 20 | 10 | 0.20 |
20≤x< 30 | 16 | b |
30≤x< 40 | a | 0.24 |
x≥ 40 | 4 | 0.08 |

其中,应急执勤次数在20≤x< 30这一组的数据是:
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
请根据所给信息,解答下列问题:
(1)![]() = ,
= ,![]() = ;
= ;
(2)请补全频数分布直方图;
(3)随机抽取的50名在职党员参加应急执勤次数的中位数是 ;
(4)请估计2月—3月期间A社区在职党员参加应急执勤的次数不低于30次的约有__人.
【答案】(1)a=12 b=0.32;(2)见解析;(3)23 ;(4)160.
【解析】
(1)利用数据总数与各小组的频数可得![]() ,利用频率公式可得
,利用频率公式可得![]() ;
;
(2)补全图形见解析;
(3)由各小组频数得到第25,第26个数据落在应急执勤次数在20≤x< 30这一组,根据中位数的定义可得答案;
(4)利用样本百分率估计总体即可得到答案.
解:(1)由题意得:![]()
![]()
故答案为12 ,0.32;
(2)![]()
补全图形如下,
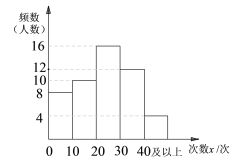
(3)因为50个排列好的数据,排在最中间的两个是第25,26个,
由题意知:这两个数据分别是23,23,所以中位数是![]()
故答案为:23.
(4)2月—3月期间A社区在职党员参加应急执勤的次数不低于30次的约有![]() 人,
人,
故答案为: 160.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】探究:如图1和2,四边形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() .
.
(1)①如图 1,若![]() 、
、![]() 都是直角,把
都是直角,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,使
,使![]() 与
与![]() 重合,则能证得
重合,则能证得![]() ,请写出推理过程;
,请写出推理过程;
②如图 2,若![]() 、
、![]() 都不是直角,则当
都不是直角,则当![]() 与
与![]() 满足数量关系_______时,仍有
满足数量关系_______时,仍有![]() ;
;
(2)拓展:如图3,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 均在边
均在边![]() 上,且
上,且![]() .若
.若![]() ,求
,求![]() 的长.
的长.
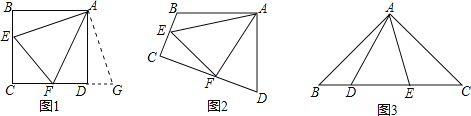
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索应用
材料一:如图1,在△ABC中,AB=c,BC=a,∠B=θ,用c和θ表示BC边上的高为 ,用a.c和θ表示△ABC的面积为 .
材料二:如图2,已知∠C=∠P,求证:CFBF=QFPF.
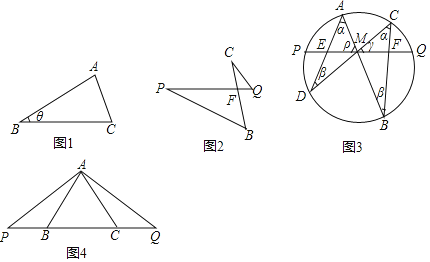
材料三:蝴蝶定理(ButterflyTheorem)是古代欧氏平面几何中最精彩的结果之一,最早出现在1815年,由W.G.霍纳提出证明,定理的图形象一只蝴蝶.
定理:如图3,M为弦PQ的中点,过M作弦AB和CD,连结AD和BC交PQ分别于点E和F,则ME=MF.
证明:设∠A=∠C=α,∠B=∠D=β,
∠DMP=∠CMQ=γ,∠AMP=∠BMQ=ρ,
PM=MQ=a,ME=x,MF=y
由![]()
即![]()
化简得:MF2AEED=ME2CFFB
则有:![]() ,
,
又∵CFFB=QFFP,AEED=PEEQ,
∴![]() ,即
,即![]()
即![]() ,从而x=y,ME=MF.
,从而x=y,ME=MF.
请运用蝴蝶定理的证明方法解决下面的问题:
如图4,B、C为线段PQ上的两点,且BP=CQ,A为PQ外一动点,且满足∠BAP=∠CAQ,判断△PAQ的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小王同学“过直线外一点作该直线的平行线”的尺规作图过程.
已知:直线l及直线l外一点P.
求作:直线![]() ,使得
,使得![]() .
.

作法:如图,
①在直线l外取一点A,作射线![]() 与直线l交于点B,
与直线l交于点B,
②以A为圆心,![]() 为半径画弧与直线l交于点C,连接
为半径画弧与直线l交于点C,连接![]() ,
,
③以A为圆心,![]() 为半径画弧与线段
为半径画弧与线段![]() 交于点
交于点![]() ,
,
则直线![]() 即为所求.
即为所求.
根据小王设计的尺规作图过程,,
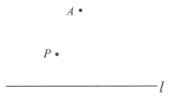
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() ,
,
∴![]() ,(______________________)(填推理的依据).
,(______________________)(填推理的依据).
∵![]() __________,
__________,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() (____________________)(填推理的依据).
(____________________)(填推理的依据).
即![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在⊙O上,弦AD的延长线与弦BC的延长线相交于点E.用①AB是⊙O的直径,②CB=CE,③AB=AE中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
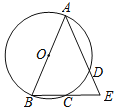
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象经过点
的图象经过点![]() (0,-4)和
(0,-4)和![]() (-2,2).
(-2,2).
(1)求![]() 的值,并用含
的值,并用含![]() 的式子表示
的式子表示![]() ;
;
(2)求证:此抛物线与![]() 轴有两个不同交点;
轴有两个不同交点;
(3)当![]() 时,若二次函数满足
时,若二次函数满足![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围;
的取值范围;
(4) 直线![]() 上有一点
上有一点![]() (
(![]() ,5),将点
,5),将点![]() 向右平移4个单位长度,得到点
向右平移4个单位长度,得到点![]() ,若抛物线与线段
,若抛物线与线段![]() 只有一个公共点,求
只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.

(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求tanC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=﹣x﹣6与x轴,y轴分别交于点A,B将直线AB沿y轴正方向平移与反比例函数y=![]() (x>0)的图象分别交于点C,D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ABE=27.
(x>0)的图象分别交于点C,D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ABE=27.
(1)求直线AC和反比例函数的解析式;
(2)连接AD,求△ACD的面积.
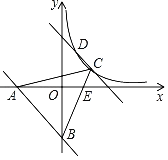
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com