
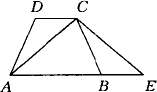
已知如图所示,梯形ABCD中,AB∥DC,AD=BC,延长AB到E,使BE=DC.求证AC=CE.
|
证法1:∵四边形ABCD是等腰梯形, ∴∠ADC=∠BCD. 又∵DC∥AB, ∴∠DCB=∠CBE. 在△ADC与△CBE中,AD=BC,∠ADC=∠CBE,DC=BE, ∴△ADC≌△CBE.∴AC=CE. 证法2:如图所示,连结DB,
∵DC∥BE,DC=BE, ∴四边形DCEB为平行四边形.∴DB=CE. 又∵四边形ABCD为等腰梯形, ∴AC=DB.∴AC=CE. 证法3:如图所示,作CF⊥AE于F,
DM⊥AE于M,在△AMD与△BFC中, ∠DAM=∠CBF,AD=BC,∠DMA=∠CFB=90°, ∴△AMD≌△BFC.∴AM=BF. 又∵DC=BE, ∴AM+MF=BF+BE. ∴F为AE中点,CF为AE的垂直平分线. ∴AC=EC. 证法4:如图所示,连结BD,
∵DC∥AB,DC=BE, ∴四边形BECD为平行四边形. ∴∠2=∠3. 又四边形ABCD是等腰梯形, ∴AC=BD. 又∵AD=BC,AB=AB, ∴△ABC≌△BAD. ∴∠1=∠2. ∴∠1=∠3,∴AC=CE. 分析:本题的证法很多.(1)由于AC与CE具有相同端点C,并且构成了△ACE,所以只需证CA=CE即可.(2)欲证AC=CE,选择一个中间量DB,证AC=DB,CE=DB即可.(3)借助线段垂直平分线的性质证AC=CE.(4)欲证AC=CE,只需证∠1=∠3,欲证∠1=∠3,只需找一中间角∠2,使∠1=∠2,∠2=∠3,所以∠1-∠3即可得证. |


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:013
已知如图所示,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为

A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:044
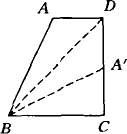
已知如图所示,梯形ABCD中,AD∥BC,DC⊥BC,沿对角线BD折叠,点A恰好落在DC上,记为![]() .若AD=4,BC=6,求的长.
.若AD=4,BC=6,求的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com