
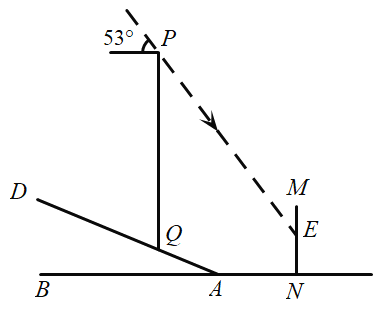
【题目】移动公司为了提升“停课不停学”期间某片区网络信号,保证广大师生网络授课、听课的质量,临时在坡度为![]() 的山坡上加装了信号塔
的山坡上加装了信号塔![]() (如图所示),信号塔底端
(如图所示),信号塔底端![]() 到坡底
到坡底![]() 的距离为3.9米.同时为了提醒市民,在距离斜坡底
的距离为3.9米.同时为了提醒市民,在距离斜坡底![]() 点4.4米的水平地面上立了一块警示牌
点4.4米的水平地面上立了一块警示牌![]() .当太阳光线与水平线成
.当太阳光线与水平线成![]() 角时,测得信号塔
角时,测得信号塔![]() 落在警示牌上的影子
落在警示牌上的影子![]() 长为3米,则信号塔
长为3米,则信号塔![]() 的高约为(结果精确到十分位,参考数据:
的高约为(结果精确到十分位,参考数据:![]() ,
,![]() ,
,![]() )
)
A.11.9米B.10.4米C.11.4米D.13.4米
【答案】A
【解析】
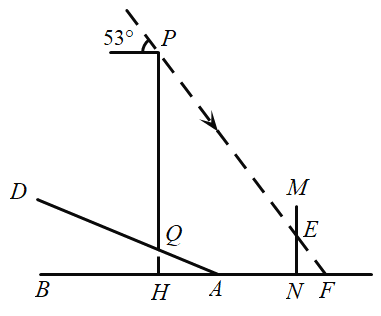
如图,延长PE,交BN于F,延长PQ,交BN于H,设QH=x米,根据坡度![]() 可求出x的值,进而可求出AH的值,根据∠HFP的正切值可求出NF的长,进而求出HF的长,利用∠HFP的正切值可求出PH的长,即可求出PQ的长.
可求出x的值,进而可求出AH的值,根据∠HFP的正切值可求出NF的长,进而求出HF的长,利用∠HFP的正切值可求出PH的长,即可求出PQ的长.
如图,延长PE,交BN于F,延长PQ,交BN于H,设QH=x米,
∵坡度![]() ,
,
∴AH=2.4x,
∵AQ=3.9,
∴x2+(2.4x)2=3.92,
解得:x=1.5,(负值舍去)
∴AH=2.4x=3.6,
∵NE=3,∠HFP=53°,
∴NF=![]() ≈
≈![]() ,
,
∴HF=AH+AN+NF=3.6+4.4+![]() =8+
=8+![]() ,
,
∴PH=HF·tan∠HFP≈(8+![]() )×1.3=13.4,
)×1.3=13.4,
∴PQ=PH-QH=11.9(米),
故选:A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
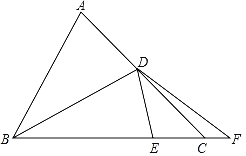
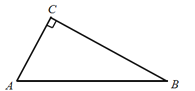
【题目】△ABC中,∠ACB=45°,D为AC上一点,AD=5![]() ,连接BD,将△ABD沿BD翻折至△EBD,点A的对应点E点恰好落在边BC上.延长BC至点F,连接DF,若CF=2,tan∠ABD=
,连接BD,将△ABD沿BD翻折至△EBD,点A的对应点E点恰好落在边BC上.延长BC至点F,连接DF,若CF=2,tan∠ABD=![]() ,则DF长为( )
,则DF长为( )
A.![]() B.
B.![]() C.5
C.5![]() D.7
D.7![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 向点
向点![]() 运动,过点
运动,过点![]() 作
作![]() 交
交![]() 的直角边于点
的直角边于点![]() ,以
,以![]() 为边向
为边向![]() 右侧作正方形
右侧作正方形![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒,正方形
秒,正方形![]() 与
与![]() 的重叠部分的面积为
的重叠部分的面积为![]() .
.
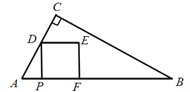
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(2)求![]() 与
与![]() 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
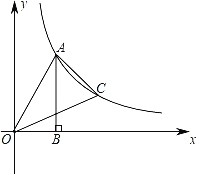
【题目】如图,点A是反比例函数y=![]() (x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan∠OAB=
(x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan∠OAB=![]() .点C是反比例函数y=
.点C是反比例函数y=![]() (x>0)图象上一动点,连接AC,OC,若△AOC的面积为
(x>0)图象上一动点,连接AC,OC,若△AOC的面积为![]() ,则点C的坐标为_____.
,则点C的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
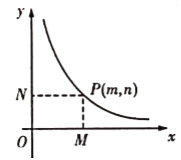
【题目】在平面直角坐标系中,等腰![]() 的底边
的底边![]() 在
在![]() 轴上,已知
轴上,已知![]() ,抛物线
,抛物线![]() (其中
(其中![]() )经过
)经过![]() 三点,双曲线
三点,双曲线![]() (其中
(其中![]() )经过点
)经过点![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 且
且![]()
(1)求出![]() 的值;当
的值;当![]() 为直角三角形时,请求出
为直角三角形时,请求出![]() 的表达式;
的表达式;
(2)当![]() 为正三角形时,直线
为正三角形时,直线![]() 平分
平分![]() ,求
,求![]() 时
时![]() 的取值范围;
的取值范围;
(3)抛物线![]() (其中
(其中![]() )有一时刻恰好经过
)有一时刻恰好经过![]() 点,且此时抛物线与双曲线
点,且此时抛物线与双曲线![]() (其中
(其中![]() )有且只有一个公共点
)有且只有一个公共点![]() (其中
(其中![]() ),我们不妨把此时刻的
),我们不妨把此时刻的![]() 记作
记作![]() ,请直接写出抛物线
,请直接写出抛物线![]() (其中
(其中![]() )与双曲线
)与双曲线![]() (其中
(其中![]() )有一个公共点时
)有一个公共点时![]() 的取值范围.(
的取值范围.(![]() 是已知数)
是已知数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,A(-4,3),B(0,1),将线段AB沿
中,A(-4,3),B(0,1),将线段AB沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位,得到线段A′B′,且A′,B′恰好都落在反比例函数
个单位,得到线段A′B′,且A′,B′恰好都落在反比例函数![]() 的图象上.
的图象上.
(1)用含![]() 的代数式表示点A′,B′的坐标;
的代数式表示点A′,B′的坐标;
(2)求![]() 的值和反比例函数
的值和反比例函数![]() 的表达式;
的表达式;
(3)点![]() 为反比例函数
为反比例函数![]() 图象上的一个动点,直线
图象上的一个动点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,请直接写出点C的坐标.
,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.

(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com