
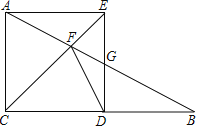
【题目】在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G,
(1)如图,点D在线段CB上,四边形ACDE是正方形.
①若点G为DE的中点,求FG的长.
②若DG=GF,求BC的长.
(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
【答案】(1)①![]() ,②12
,②12![]() ;(2)等腰
;(2)等腰![]() 的腰长为4或20或
的腰长为4或20或![]() 或
或![]() .理由见解析.
.理由见解析.
【解析】
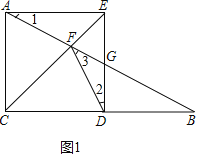
(1)①只要证明△ACF∽△GEF,推出![]() ,即可解决问题;②如图1中,想办法证明∠1=∠2=30°即可解决问题;
,即可解决问题;②如图1中,想办法证明∠1=∠2=30°即可解决问题;
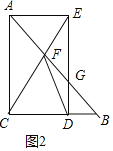
(2)分四种情形:①如图2中,当点D在线段BC上时,此时只有GF=GD,②如图3中,当点D在线段BC的延长线上,且直线AB,CE的交点中AE上方时,此时只有GF=DG,
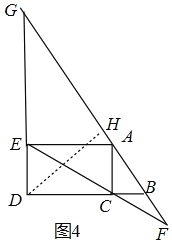
③如图4中,当点D在线段BC的延长线上,且直线AB,EC的交点中BD下方时,此时只有DF=DG,如图5中,当点D中线段CB的延长线上时,此时只有DF=DG,分别求解即可解决问题.
(1)①在正方形![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
②如图1中,
正方形![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,设
,设![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
![]() 在
在![]() 中,
中,![]() .
.
(2)在![]() 中,
中,![]() ,
,
如图2中,
当点![]() 在线段
在线段![]() 上时,此时只有
上时,此时只有![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
整理得:![]() ,
,
解得![]() 或5(舍弃)
或5(舍弃)
![]() 腰长
腰长![]() .
.
如图3中,

当点![]() 在线段
在线段![]() 的延长线上,且直线
的延长线上,且直线![]() ,
,![]() 的交点中
的交点中![]() 上方时,此时只有
上方时,此时只有![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
解得![]() 或
或![]() (舍弃),
(舍弃),
![]() 腰长
腰长![]() .
.
如图4中,
当点![]() 在线段
在线段![]() 的延长线上,且直线
的延长线上,且直线![]() ,
,![]() 的交点中
的交点中![]() 下方时,此时只有
下方时,此时只有![]() ,过点
,过点![]() 作
作![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
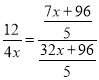 ,
,
解得![]() 或
或![]() (舍弃)
(舍弃)
![]() 腰长
腰长![]() ,
,
如图5中,
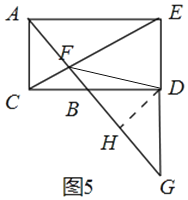
当点![]() 在线段
在线段![]() 的延长线上时,此时只有
的延长线上时,此时只有![]() ,作
,作![]() 于
于![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
 ,
,
解得![]() 或
或![]() (舍弃),
(舍弃),
![]() 腰长
腰长![]() ,
,
综上所述,等腰![]() 的腰长为4或20或
的腰长为4或20或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】为积极响应党和国家精准扶贫战略计划,某公司在农村租用了 720亩闲置土地种植了乔 木型、小乔木型和灌木型三种茶树. 为达到最佳种植收益,要求种植乔木型茶树的面积是小乔木型茶树面积的2倍,灌木型茶树的面积不得超过乔木型茶树面积的![]() 倍,但种植乔木型茶树的面积不得超过270亩. 到茶叶采摘季节时,该公司聘请当地农民进行采摘,每人每天可以采摘0.4亩乔木型茶叶,或者采摘0.5亩小乔木型茶叶,或者采摘0.6亩灌木型茶叶. 若该公司聘请一批农民恰好20天能采摘完所有茶叶,则种植乔木型茶树的面积是________亩.
倍,但种植乔木型茶树的面积不得超过270亩. 到茶叶采摘季节时,该公司聘请当地农民进行采摘,每人每天可以采摘0.4亩乔木型茶叶,或者采摘0.5亩小乔木型茶叶,或者采摘0.6亩灌木型茶叶. 若该公司聘请一批农民恰好20天能采摘完所有茶叶,则种植乔木型茶树的面积是________亩.
查看答案和解析>>
科目:初中数学 来源: 题型:
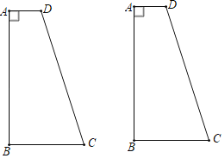
【题目】如图所示,四边形ABCD中,AD∥BC,∠A=90°,∠BCD<90°,AB=7,AD=2,BC=3,试在边AB上确定点P的位置,使得以P、C、D为顶点的三角形是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
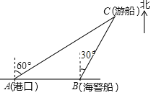
【题目】一艘观光游船从港口![]() 以北偏东
以北偏东![]() 的方向出港观光,航行
的方向出港观光,航行![]() 海里至
海里至![]() 处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东
处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东![]() 方向,马上以
方向,马上以![]() 海里每小时的速度前往救援,海警船到达事故船
海里每小时的速度前往救援,海警船到达事故船![]() 处所需的时间大约为________小时(用根号表示).
处所需的时间大约为________小时(用根号表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3,则下列结论不一定成立的是( )
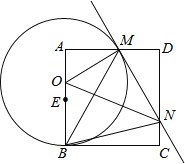
A.S1>S2+S3 B.△AOM∽△DMN C.∠MBN=45° D.MN=AM+CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒2
边上以每秒2![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]()
![]() 的速度向点
的速度向点![]() 匀速运动,设运动时间为
匀速运动,设运动时间为![]() (
(![]() ),连接
),连接![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 与
与![]() 相似,求
相似,求![]() 的值;
的值;
(3)当![]() 为何值时,四边形
为何值时,四边形![]() 的面积最小?并求出最小值.
的面积最小?并求出最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 随机抛掷一枚均匀的硬币,落地后反面一定朝上。
B. 从1,2,3,4,5中随机取一个数,取得奇数的可能性较大。
C. 某彩票中奖率为![]() ,说明买100张彩票,有36张中奖。
,说明买100张彩票,有36张中奖。
D. 打开电视,中央一套正在播放新闻联播。
查看答案和解析>>
科目:初中数学 来源: 题型:
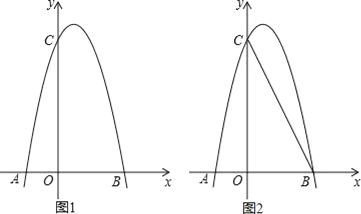
【题目】如图1,对称轴为直线x=![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,底边BC长为8,腰长为6,点D是BC边上一点,过点B作AC的平行线与过A、B、D三点的圆交于点E,连接DE,则DE的最小值是___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com