
分析 (1)用每件的利润(x-20)乘以销售量即可得到每天的销售利润,即w=(x-20)y=(x-20)(-2x+80),然后化为一般式即可;
(2)把(1)中的解析式进行配方得到顶点式y=-2(x-30)2+200,然后根据二次函数的最值问题求解;
(3)求函数值为150所对应的自变量的值,即解方程-2(x-30)2+200=150,然后利用销售价不高于每件28元确定x的值.
解答 解:(1)根据题意可得:w=(x-20)•y
=(x-20)(-2x+80)
=-2x2+120x-1600,
w与x的函数关系式为:w=-2x2+120x-1600;
(2)根据题意可得:w=-2x2+120x-1600=-2(x-30)2+200,
∵-2<0,∴当x=30时,w有最大值.w最大值为200.
答:销售单价定为30元时,每天销售利润最大,最大销售利润200元.
(3)当w=150时,可得方程-2(x-30)2+200=150.
解得 x1=25,x2=35.
∵35>28,∴x2=35不符合题意,应舍去.
答:该商店销售这种健身球每天想要获得150元的销售利润,销售单价定为25元.
点评 本题考查了二次函数的实际应用:利用二次函数解决利润问题,在商品经营活动中,经常会遇到求最大利润,最大销量等问题.解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
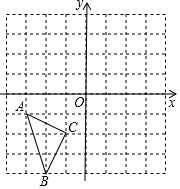 △ABC在平面直角坐标系中的位置如图所示
△ABC在平面直角坐标系中的位置如图所示查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
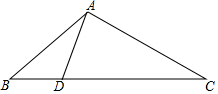 如图,将①∠BAD=∠C;②∠ADB=∠CAB;③AB2=BD•BC;④$\frac{CA}{AD}$=$\frac{AB}{DB}$;⑤$\frac{BC}{BA}$=$\frac{DA}{AC}$中的一个作为条件,另一个作为结论,组成一个真命题.
如图,将①∠BAD=∠C;②∠ADB=∠CAB;③AB2=BD•BC;④$\frac{CA}{AD}$=$\frac{AB}{DB}$;⑤$\frac{BC}{BA}$=$\frac{DA}{AC}$中的一个作为条件,另一个作为结论,组成一个真命题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
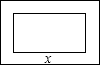 在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )
在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )| A. | (50-x)(80-x)=5400 | B. | (50-2x)(80-2x)=5400 | C. | (50+x)(80+x)=5400 | D. | (50+2x)(80+2x)=5400 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com