7.5 25 30 15
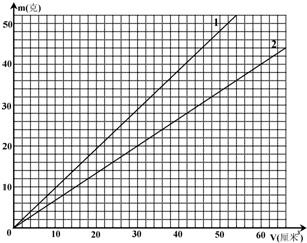
分析:图象中纵坐标表示物质的质量,横坐标表示物质的体积,过坐标原点的直线的斜率即表示物质的密度,从而可以根据图象计算出1、2两种物质的密度,而甲放入乙中时,甲浮在液面上,根据物体的浮沉条件可以判断出甲、乙两种物质的密度,物块甲恰好被液体全部浸没(v
排=v),根据阿基米德原理求出此时物块甲受到的浮力,因为此时物块甲受到的浮力等于物块甲的重加上物体A的重,即F
浮=G
排=G
甲+G
A,可以化简为:m
排g=m
1g+m
2g,即m
排=m
1+m
2,据此求物块甲、A的质量.
解答:
图象中纵坐标表示物质的质量,横坐标表示物质的体积,过坐标原点的直线的斜率即表示物质的密度,
从图可知,当1物质的质量为12g时,体积为12cm
3,ρ
1=
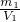
=
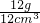
=1g/cm
3,
当2物质的质量为8g时,体积为12cm
3,ρ
2=
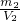
=
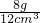
=

g/cm
3,
而甲放入乙中时,甲浮在液面上,根据物体的浮沉条件可知:ρ
乙>ρ
甲,
从而可知,ρ
乙=ρ
1=1g/cm
3,ρ
甲=ρ
2=

g/cm
3,
∵物块甲恰好被液体全部浸没(v
排=v
甲),
∴此时物块甲受到的浮力等于物块甲的重加上物体A的重,即F
浮=G
排=G
甲+G
A,
可以化简为:m
排g=m
1g+m
2g,即m
排=m
1+m
2,
第一组:当m
甲=m
1=15g时,
则V
排=V
1=V
甲=

=
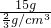
=22.5cm
3,
m
排=ρ
乙V
排=ρ
乙V
甲=1g/cm
3×22.5cm
3=22.5g,
∴m
2=m
排-m
1=22.5g-15g=7.5g.
第二组:设此时甲的体积为V甲2,
而m
排=m
1+m
2,
即:ρ
乙V
排=ρ
乙V
甲2=ρ
甲V
甲2+m
2,而m
2=12.5g,
代入数值得:1g/cm
3×V
甲2=

g/cm
3×V
甲2+12.5g,
解得:V
甲2=37.5cm
3,
此时m
1=ρ
甲V
甲2=

g/cm
3×37.5cm
3=25g.
第三组:当m
甲=m
1=30g时,
则V
排=V
1=V
甲=

=
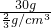
=45cm
3,
m
排=ρ
乙V
排=ρ
乙V
甲=1g/cm
3×45cm
3=45g,
∴m
2=m
排-m
1=45g-30g=15g.
故答案为:7.5;25;30,15.
点评:本题考查了密度的特性及应用数学函数图象来分析解决物理问题的能力.解决此类图象问题时,可采取控制变量思想,取相同体积来比较质量或取相同质量为比较体积.以及对阿基米德原理和物体浮沉条件的理解和应用.

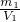 =
=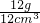 =1g/cm3,
=1g/cm3,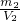 =
=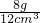 =
= g/cm3,
g/cm3, g/cm3,
g/cm3, =
=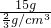 =22.5cm3,
=22.5cm3, g/cm3×V甲2+12.5g,
g/cm3×V甲2+12.5g, g/cm3×37.5cm3=25g.
g/cm3×37.5cm3=25g.  =
=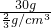 =45cm3,
=45cm3,

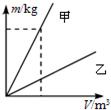 小华同学在探究甲、乙两种物质的质量跟体积的关系时,做出了如图所示的图象.根据图象提供的信息,以下说法中不正确的是( )
小华同学在探究甲、乙两种物质的质量跟体积的关系时,做出了如图所示的图象.根据图象提供的信息,以下说法中不正确的是( )

 如图所示是甲、乙两种物质的质量跟体积关系的图象,根据图象分析可知,密度ρ甲
如图所示是甲、乙两种物质的质量跟体积关系的图象,根据图象分析可知,密度ρ甲