
 图是某水上打捞船起吊装置结构示意简图.某次打捞作业中,该船将沉没于水下深处的一只密封货箱以0.1m/s的速度匀速打捞出水面,已知该货箱体积为50m3,质量是200t.( g取10N/kg,忽略钢缆绳重及其与滑轮间的摩擦,不考虑风浪、水流等因素的影响.)
图是某水上打捞船起吊装置结构示意简图.某次打捞作业中,该船将沉没于水下深处的一只密封货箱以0.1m/s的速度匀速打捞出水面,已知该货箱体积为50m3,质量是200t.( g取10N/kg,忽略钢缆绳重及其与滑轮间的摩擦,不考虑风浪、水流等因素的影响.) =
= =80%;
=80%; (G物+G轮)
(G物+G轮) (G物+G轮-F浮)=
(G物+G轮-F浮)= (2×106N+5×105N-5×105N)=5×105N,
(2×106N+5×105N-5×105N)=5×105N, (G物+G轮)求动滑轮重;露出水面前,物体受到水的浮力,利用F=
(G物+G轮)求动滑轮重;露出水面前,物体受到水的浮力,利用F= (G物+G轮-F浮)求此时的拉力,求出拉力端移动的速度,利用P=Fv求钢缆绳拉力的功率.
(G物+G轮-F浮)求此时的拉力,求出拉力端移动的速度,利用P=Fv求钢缆绳拉力的功率. (G物+G轮-F浮),物体露出水面后拉力F=
(G物+G轮-F浮),物体露出水面后拉力F= (G物+G轮).
(G物+G轮). 

科目:初中物理 来源: 题型:
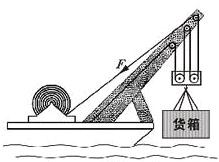 如图是某水上打捞船起吊装置结构示意简图.某次打捞作业中,该船将沉没于水下深处的一只密封货箱打捞出水面,已知该货箱体积为50m3,质量是200t.
如图是某水上打捞船起吊装置结构示意简图.某次打捞作业中,该船将沉没于水下深处的一只密封货箱打捞出水面,已知该货箱体积为50m3,质量是200t.查看答案和解析>>
科目:初中物理 来源: 题型:
 (2011?名山县模拟)图是某水上打捞船起吊装置结构示意简图.某次打捞作业中,该船将沉没于水下深处的一只密封货箱以0.1m/s的速度匀速打捞出水面,已知该货箱体积为50m3,质量是200t.( g取10N/kg,忽略钢缆绳重及其与滑轮间的摩擦,不考虑风浪、水流等因素的影响.)
(2011?名山县模拟)图是某水上打捞船起吊装置结构示意简图.某次打捞作业中,该船将沉没于水下深处的一只密封货箱以0.1m/s的速度匀速打捞出水面,已知该货箱体积为50m3,质量是200t.( g取10N/kg,忽略钢缆绳重及其与滑轮间的摩擦,不考虑风浪、水流等因素的影响.)查看答案和解析>>
科目:初中物理 来源: 题型:
 (2010?营口)如图是某水上打捞船起吊装置结构示意图.某次打捞作业中,该船将沉没于水下深处的一只密封货箱打捞出水面,已知该货箱体积为50m3,质量是200t.
(2010?营口)如图是某水上打捞船起吊装置结构示意图.某次打捞作业中,该船将沉没于水下深处的一只密封货箱打捞出水面,已知该货箱体积为50m3,质量是200t.查看答案和解析>>
科目:初中物理 来源: 题型:
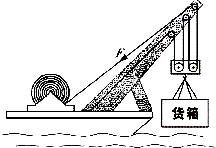 如图是某水上打捞船起吊装置结构示意简图.某次打捞作业中,该船将沉没于水下深处的一只密封货箱打捞出水面,已知该货箱体积为5m3,质量是20t
如图是某水上打捞船起吊装置结构示意简图.某次打捞作业中,该船将沉没于水下深处的一只密封货箱打捞出水面,已知该货箱体积为5m3,质量是20t查看答案和解析>>
科目:初中物理 来源:2009年江西省南昌市中考物理模拟试卷(三)(解析版) 题型:解答题
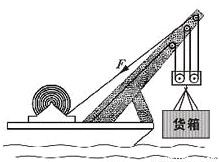
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com