
 (1)甲、乙是两个体积相同而材料不同的实心球,它们静止在某种液体中的情况如图5所示.那么两球所受浮力F甲______F乙,两球的密度ρ甲______ρ乙.(选填“>”、“<”或“=”)
(1)甲、乙是两个体积相同而材料不同的实心球,它们静止在某种液体中的情况如图5所示.那么两球所受浮力F甲______F乙,两球的密度ρ甲______ρ乙.(选填“>”、“<”或“=”)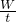 =
=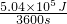 =140W.
=140W.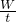 计算出学生的散热功率.
计算出学生的散热功率.

 阅读快车系列答案
阅读快车系列答案科目:初中物理 来源: 题型:
 10、甲、乙是两个体积相同而材料不同的实心球,它们静止在某种液体中的情况如图所示.那么两球所受浮力F甲
10、甲、乙是两个体积相同而材料不同的实心球,它们静止在某种液体中的情况如图所示.那么两球所受浮力F甲查看答案和解析>>
科目:初中物理 来源: 题型:
 (2007?越秀区一模)(1)甲、乙是两个体积相同而材料不同的实心球,它们静止在某种液体中的情况如图5所示.那么两球所受浮力F甲
(2007?越秀区一模)(1)甲、乙是两个体积相同而材料不同的实心球,它们静止在某种液体中的情况如图5所示.那么两球所受浮力F甲查看答案和解析>>
科目:初中物理 来源:2007年广东省广州市越秀区中考物理一模试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com