
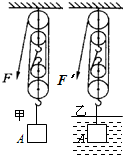
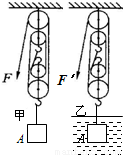
 如图,正方体A的边长为0.1m,密度为8×103kg/m3.将此物体挂在如图所示的滑轮组上,不计绳重与摩擦,则:
如图,正方体A的边长为0.1m,密度为8×103kg/m3.将此物体挂在如图所示的滑轮组上,不计绳重与摩擦,则: =
=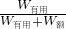 =
=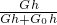 =
=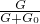 =
=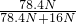 ≈83%;
≈83%; ,绳子拉下的长度是物体上升高度的4倍,拉力和绳子拉下长度之积是拉力做的功,拉力做的功与所用时间之比就是拉力的功率.
,绳子拉下的长度是物体上升高度的4倍,拉力和绳子拉下长度之积是拉力做的功,拉力做的功与所用时间之比就是拉力的功率. (G+G0)=
(G+G0)= ×(78.4N+16N)=23.6N
×(78.4N+16N)=23.6N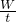 =
=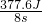 =47.2W;
=47.2W;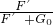 =
=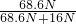 ≈81%.
≈81%.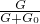 计算滑轮组机械效率.
计算滑轮组机械效率.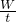 得到拉力的功率;
得到拉力的功率;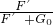 计算此时滑轮组机械效率.
计算此时滑轮组机械效率.

 名校课堂系列答案
名校课堂系列答案科目:初中物理 来源: 题型:
 (2012?青岛模拟)如图,正方体A的边长为0.1m,密度为8×103kg/m3.将此物体挂在如图所示的滑轮组上,不计绳重与摩擦,则:
(2012?青岛模拟)如图,正方体A的边长为0.1m,密度为8×103kg/m3.将此物体挂在如图所示的滑轮组上,不计绳重与摩擦,则:查看答案和解析>>
科目:初中物理 来源: 题型:
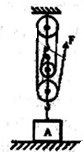 如图所示,正方体A在水平地面上处于静止状态,已知动滑轮总重为3N,作用在绳端的拉力F为5.5N,正方体A的边长为10cm,A对水平地面产生的压强为800Pa,则A物体的密度为:(忽略摩擦和绳重,绳对滑轮的拉力方向均可看成在竖直方向,g=10N/kg)( )
如图所示,正方体A在水平地面上处于静止状态,已知动滑轮总重为3N,作用在绳端的拉力F为5.5N,正方体A的边长为10cm,A对水平地面产生的压强为800Pa,则A物体的密度为:(忽略摩擦和绳重,绳对滑轮的拉力方向均可看成在竖直方向,g=10N/kg)( )查看答案和解析>>
科目:初中物理 来源: 题型:
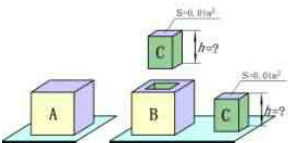 如图所示,密度均匀的正方体A的边长为0.2米,质量为16千克.求:
如图所示,密度均匀的正方体A的边长为0.2米,质量为16千克.求:查看答案和解析>>
科目:初中物理 来源:2012年山东省青岛市中考物理调研试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com