

| 甲图中砝码和游码总质量值m1/g | 乙图中砝码和游码总质量值m2/g | 乙图中弹簧测力计示数F/N | 金属球的体积V/cm3 | 金属球的质量m/g | 金属球的密度ρ/g/cm3 |
| 80 | ________ | ________ | ________ | ________ | ________ |
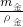 g)L1=m码gL3,
g)L1=m码gL3,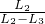 ρ水;
ρ水;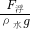 =
=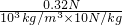 =0.32×10-4m3=32cm3
=0.32×10-4m3=32cm3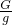 =
=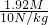 =0.192kg=192g;
=0.192kg=192g;  =
= =6g/cm3
=6g/cm3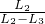 ρ水;
ρ水;

 学习实践园地系列答案
学习实践园地系列答案科目:初中物理 来源: 题型:
 (2010?西城区二模)测定组成实心金属球金属的密度.如图所示,杠杆的重力忽略不计,请你将下列实验步骤补充完整.
(2010?西城区二模)测定组成实心金属球金属的密度.如图所示,杠杆的重力忽略不计,请你将下列实验步骤补充完整.| L2 |
| L2-L3 |
| L2 |
| L2-L3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com