精英家教网> 2026年优课堂给力A加八年级数学上册北师大版 > 第1页 参考答案
2026年优课堂给力A加八年级数学上册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册2026年优课堂给力A加八年级数学上册北师大版答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.勾股定理:直角三角形
两直角边的平方和等于斜边的平方
。如果用$a$,$b$和$c$分别表示直角三角形的两直角边和斜边,那么
$a^{2}+b^{2}=c^{2}$
。
2.应用勾股定理的注意事项
(1)勾股定理使用的前提是在直角三角形中;
(2)要分清直角边和斜边,在$Rt\triangle ABC$中,直角不一定是$\angle C$,也就是$c$不一定是斜边。
认识勾股定理
答案:两直角边的平方和等于斜边的平方;$a^{2}+b^{2}=c^{2}$
解析:
勾股定理是直角三角形的重要性质,其内容为两直角边的平方和等于斜边的平方。用字母表示时,若两直角边为$a$、$b$,斜边为$c$,则关系式为$a^{2}+b^{2}=c^{2}$。
【例1】下列说法中正确的是 (
C
)
A.已知$a$,$b$,$c$是三角
形
的三边,则$a^{2}+b^{2}=c^{2}$
B.在直角三角形中两边和的平方等于第三边的平方
C.在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,则$BC^{2}+AC^{2}=AB^{2}$
D.在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,则$BC^{2}+AC^{2}=AB^{2}$
答案:C
解析:
A. 没有说明三角形是直角三角形,也没有说明$c$是斜边,所以A选项错误。
B. 在直角三角形中,必须是两条直角边的平方和等于斜边的平方,而不是两边和的平方等于第三边的平方,所以B选项错误。
C. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,根据勾股定理,两条直角边的平方和等于斜边的平方,即$BC^{2} + AC^{2} = AB^{2}$,所以C选项正确。
D. 在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,则$AC$是斜边,应该是$BC^{2} + AB^{2} = AC^{2}$,而不是$BC^{2} + AC^{2} = AB^{2}$,所以D选项错误。
1.某直角三角形的两条边长分别是3和5,那么第三条边长的平方为
16或34
。
答案:$16$或$34$
解析:
本题可根据勾股定理,结合直角三角形两条边长分别是$3$和$5$,分情况讨论第三条边为斜边或直角边时的情况。
勾股定理是指直角三角形两直角边的平方和等于斜边的平方。
情况一:当$5$是斜边时
设另一条直角边为$x$,根据勾股定理可得$x^{2}=5^{2}-3^{2}=25 - 9 = 16$。
情况二:当$5$和$3$都是直角边时
设斜边为$y$,根据勾股定理可得$y^{2}=3^{2}+5^{2}=9 + 25 = 34$。
2. 如图,在$\triangle ABC$中,已知$\angle C=90^{\circ}$,$a$,$b$,$c$是$\triangle ABC$的三边长。
(1)若$c = 25$,$a = 7$,则$b =$
24
;
(2)若$c = 40$,$a:b = 3:4$,则$a =$
24
,$b =$
32
。
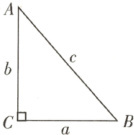
答案:24;24;32
解析:
(1)在Rt△ABC中,∠C=90°,由勾股定理得$a^2 + b^2 = c^2$。已知$c=25$,$a=7$,则$b = \sqrt{c^2 - a^2} = \sqrt{25^2 - 7^2} = \sqrt{625 - 49} = \sqrt{576} = 24$。
(2)设$a=3k$,$b=4k$($k>0$)。由勾股定理得$(3k)^2 + (4k)^2 = c^2$,即$9k^2 + 16k^2 = 40^2$,$25k^2 = 1600$,$k^2 = 64$,$k=8$。所以$a=3×8=24$,$b=4×8=32$。
【例2】如图所示的是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是 (
C
)
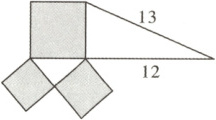
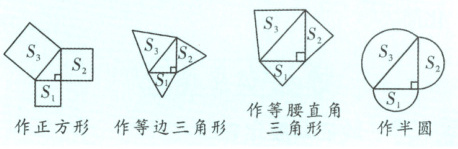
【方法点拨】巧用勾股定理求面积:以两直角边为边长(或直径)所作的两个图形的面积和等于以斜边为边长(或直径)所作图形的面积,即$S_{3}=S_{1}+S_{2}$。
A.50
B.16
C.25
D.41
答案:C
解析:
根据勾股定理,对应面积关系为 $S_3 = S_1 + S_2$。
由图示可知,直角三角形斜边为 13,一个直角边为 12。
根据勾股定理,另一条直角边为:
$\sqrt{13^2 - 12^2} = \sqrt{169 - 144} = \sqrt{25} = 5$,
阴影部分对应 $S_2$,即边长为 5 的正方形面积:
$S_2 = 5^2 = 25$。
3. 如图,三个正方形围成一个直角三角形,图中的数据是它们的面积,则正方形A的边长为 (
C
)
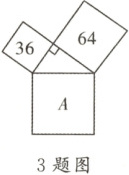
A.6
B.8
C.10
D.12
答案:C
解析:
设直角三角形的两条直角边对应的正方形面积分别为36和64,斜边对应的正方形面积为A的面积。根据勾股定理,直角三角形两条直角边的平方和等于斜边的平方,即两个小正方形的面积和等于大正方形的面积。所以正方形A的面积为36+64=100,其边长为√100=10。
4. 如图,以一个直角三角形的三边为直径向外作3个半圆。已知半圆A,B的直径长分别是$a$,$b$,直角三角形的斜边长为$c$。
(1)$S_{A}=$
$\frac{\pi a^{2}}{8}$
;$S_{B}=$
$\frac{\pi b^{2}}{8}$
;
(
2)
若$S_{A}=6$,$S_{B}=8$,
则$S_{C}=$
14
。
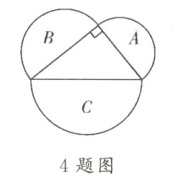
答案:$\frac{\pi a^{2}}{8}$;$\frac{\pi b^{2}}{8}$;14
解析:
(1) 半圆A的直径为a,半径为$\frac{a}{2}$,面积$S_{A}=\frac{1}{2}\pi(\frac{a}{2})^{2}=\frac{\pi a^{2}}{8}$;半圆B的直径为b,半径为$\frac{b}{2}$,面积$S_{B}=\frac{1}{2}\pi(\frac{b}{2})^{2}=\frac{\pi b^{2}}{8}$。
(2) 由勾股定理得$a^{2}+b^{2}=c^{2}$。半圆C的直径为c,半径为$\frac{c}{2}$,面积$S_{C}=\frac{1}{2}\pi(\frac{c}{2})^{2}=\frac{\pi c^{2}}{8}$。因为$S_{A}+S_{B}=\frac{\pi a^{2}}{8}+\frac{\pi b^{2}}{8}=\frac{\pi(a^{2}+b^{2})}{8}=\frac{\pi c^{2}}{8}=S_{C}$,所以$S_{C}=6+8=14$。





