精英家教网> 2025年学典四川九年级数学全一册北师大版 > 第2页 参考答案
2025年学典四川九年级数学全一册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册2025年学典四川九年级数学全一册北师大版答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,菱形 $ABCD$ 中,已知 $\angle ABD = 20^{\circ}$,则 $\angle C$ 的度数是(
D
)
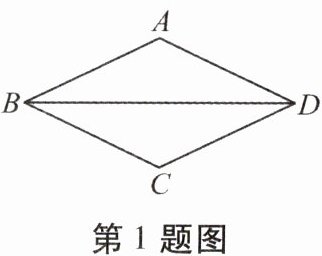
A.$40^{\circ}$
B.$80^{\circ}$
C.$120^{\circ}$
D.$140^{\circ}$
答案:D
解析:
解:在菱形$ABCD$中,$AB = AD$,$\angle A+\angle C=180^{\circ}$。
$\triangle ABD$中,$\angle ABD = 20^{\circ}$,则$\angle ADB=\angle ABD = 20^{\circ}$。
$\angle A=180^{\circ}-\angle ABD-\angle ADB=180^{\circ}-20^{\circ}-20^{\circ}=140^{\circ}$。
$\angle C=180^{\circ}-\angle A=180^{\circ}-140^{\circ}=40^{\circ}$。
A
2. 如图,在菱形 $ABCD$ 中,点 $E$,$F$ 分别是 $AC$,$AB$ 的中点,如果 $EF = 3$,那么菱形 $ABCD$ 的周长为(
A
)
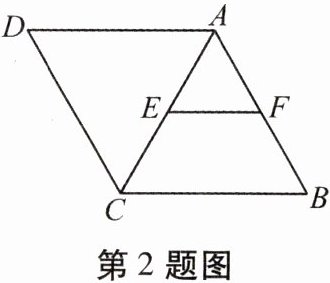
A.$24$
B.$18$
C.$12$
D.$9$
答案:A
解析:
在菱形$ABCD$中,$AB=BC=CD=DA$。
因为点$E$,$F$分别是$AC$,$AB$的中点,所以$EF$是$\triangle ABC$的中位线。
根据三角形中位线定理,$EF=\frac{1}{2}BC$。
已知$EF = 3$,则$\frac{1}{2}BC=3$,解得$BC=6$。
菱形$ABCD$的周长为$4× BC=4×6 = 24$。
A
3. 如图,菱形 $ABCD$ 对角线的交点与坐标原点 $O$ 重合,已知点 $A$ 的坐标为 $(-2,5)$,则点 $C$ 的坐标是(
B
)

A.$(5,-2)$
B.$(2,-5)$
C.$(2,5)$
D.$(-2,-5)$
答案:B
解析:
在菱形$ABCD$中,对角线互相平分,交点为坐标原点$O$,则点$A$与点$C$关于原点对称。
已知点$A$的坐标为$(-2,5)$,关于原点对称的点的坐标特点是横、纵坐标均互为相反数,所以点$C$的坐标为$(2,-5)$。
B
4. 如图,在平面直角坐标系中,菱形 $OACB$ 的顶点 $O$ 与原点重合,若点 $C$ 的坐标为 $(4,0)$,点 $B$ 的纵坐标是 $-1$,则菱形 $OACB$ 的顶点 $A$ 的坐标是______
(2,1)
.

答案:(2,1)
解析:
∵菱形$OACB$的顶点$O$与原点重合,对角线$OC$与$AB$相交于点$D$。
∵点$C$的坐标为$(4,0)$,
∴$OC$在$x$轴上,$OC=4$,$OD=\frac{1}{2}OC=2$,即点$D$的横坐标为$2$。
∵菱形的对角线互相平分,
∴点$D$是$AB$的中点。
设点$A$的坐标为$(x,y)$,点$B$的坐标为$(m,-1)$。
∵点$D$是$AB$的中点,
∴$\frac{x+m}{2}=2$,$\frac{y+(-1)}{2}$为点$D$的纵坐标。
又
∵$OC$与$AB$互相垂直平分,$OC$在$x$轴上,
∴$AB$垂直于$x$轴,即点$A$和点$B$的横坐标相同,$x=m$。
由$\frac{x+x}{2}=2$,得$x=2$。
∵$AB$垂直于$x$轴,$D$为$AB$中点,$OD=2$,$B$的纵坐标为$-1$,
∴$\frac{y+(-1)}{2}=0$($D$在$x$轴上,纵坐标为$0$),解得$y=1$。
∴点$A$的坐标是$(2,1)$。
$(2,1)$
5. 如图,在菱形 $ABCD$ 外侧作等边三角形 $CBE$,连接 $DE$,$AE$。若 $\angle ABC = 100^{\circ}$,则 $\angle EDC$ 的度数为
$20^{\circ}$
.

答案:$20^{\circ}$
解析:
∵四边形$ABCD$是菱形,
$\therefore CD = CB$,$\angle ADC=\angle ABC = 100^{\circ}$,$\angle BCD=180^{\circ}-\angle ABC=80^{\circ}$。
∵$\triangle CBE$是等边三角形,
$\therefore CB = CE$,$\angle BCE=60^{\circ}$。
$\therefore CD=CE$,$\angle DCE=\angle BCD+\angle BCE=80^{\circ}+60^{\circ}=140^{\circ}$。
在$\triangle DCE$中,$CD = CE$,
$\therefore \angle EDC=\frac{180^{\circ}-\angle DCE}{2}=\frac{180^{\circ}-140^{\circ}}{2}=20^{\circ}$。
$20^{\circ}$
6. 如图,菱形 $ABCD$ 的边长为 $2$,$\angle ABC = 60^{\circ}$,对角线 $AC$ 与 $BD$ 交于点 $O$,$E$ 为 $OB$ 的中点,$F$ 为 $AD$ 的中点,连接 $EF$,则 $EF$ 的长为
$\frac{\sqrt{13}}{2}$
.
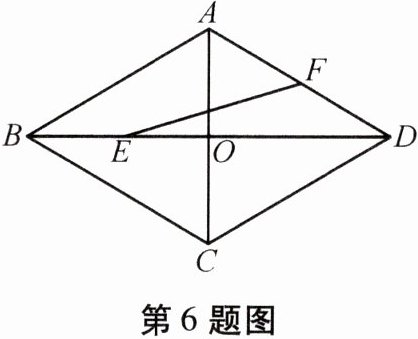
答案:$\frac{\sqrt{13}}{2}$
解析:
解:
∵菱形 $ABCD$ 边长为 $2$,$\angle ABC=60^\circ$,
∴$\triangle ABC$ 为等边三角形,$AC=AB=2$,$BD \perp AC$,$O$ 为 $AC$、$BD$ 中点,
∴$AO=OC=1$,$BO=DO=\sqrt{AB^2 - AO^2}=\sqrt{2^2 - 1^2}=\sqrt{3}$。
以 $O$ 为原点,$AC$ 为 $x$ 轴,$BD$ 为 $y$ 轴建立坐标系,
则 $A(-1,0)$,$D(0,\sqrt{3})$,$B(0,-\sqrt{3})$。
∵$E$ 为 $OB$ 中点,$F$ 为 $AD$ 中点,
∴$E\left(0,-\frac{\sqrt{3}}{2}\right)$,$F\left(\frac{-1+0}{2},\frac{0+\sqrt{3}}{2}\right)=\left(-\frac{1}{2},\frac{\sqrt{3}}{2}\right)$。
∴$EF=\sqrt{\left(-\frac{1}{2}-0\right)^2 + \left(\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}\right)^2}=\sqrt{\left(-\frac{1}{2}\right)^2 + (\sqrt{3})^2}=\sqrt{\frac{1}{4}+3}=\frac{\sqrt{13}}{2}$。
$\frac{\sqrt{13}}{2}$
7. 如图,在菱形 $ABCD$ 中,$AE \perp CD$,垂足为 $E$,$CF \perp AD$,垂足为 $F$。求证:$AF = CE$。

答案:证明:
∵四边形ABCD是菱形,
∴AD=CD,∠D=∠D(公共角)。
∵AE⊥CD,CF⊥AD,
∴∠AED=∠CFD=90°。
在△AED和△CFD中,
∠AED=∠CFD,
∠D=∠D,
AD=CD,
∴△AED≌△CFD(AAS)。
∴DE=DF。
∵AD=CD,
∴AD-DF=CD-DE,即AF=CE。







