精英家教网> 2025年云南省标准教辅优佳学案配套测试卷八年级数学上册人教版 > 第1页 参考答案
2025年云南省标准教辅优佳学案配套测试卷八年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册2025年云南省标准教辅优佳学案配套测试卷八年级数学上册人教版答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列图形中,具有稳定性的是(
B
).
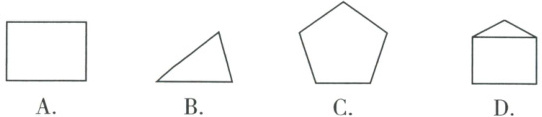
答案:B
解析:
三角形具有稳定性,四边形及多边形不具有稳定性。选项A是四边形,B是三角形,C是五边形,D是组合图形(含四边形),故具有稳定性的是B。
2. 已知下列各组中三条线段的长度,其中不能组成三角形的是(
C
).
A.2 cm,3 cm,4 cm
B.3 cm,6 cm,6 cm
C.2 cm,2 cm,6 cm
D.5 cm,6 cm,7 cm
答案:C
解析:
要判断三条线段能否组成三角形,需满足三角形两边之和大于第三边的条件。
对选项逐一验证:
A. 2 + 3 > 4,2 + 4 > 3,3 + 4 > 2,满足条件;
B. 3 + 6 > 6,3 + 6 > 6,6 + 6 > 3,满足条件;
C. 2 + 2 < 6(不满足),因此不能组成三角形;
D. 5 + 6 > 7,5 + 7 > 6,6 + 7 > 5,满足条件。
3. 下面四个图形中,线段$AD$是$\triangle ABC$中边$BC$上的高的图形为(
C
).
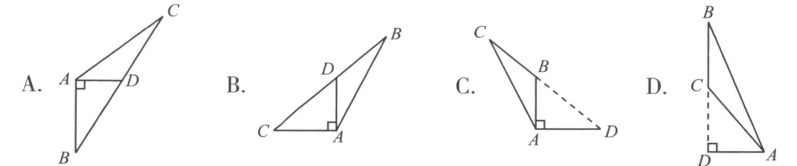
答案:C
解析:
根据三角形高的定义,过顶点A向对边BC所在直线作垂线,垂足为D,则AD是BC边上的高。选项C中,AD垂直于BC,垂足为D,符合定义。
4. 如图,直线$AB// CD$,且$AC\perp BC$于点$C$.若$\angle BAC = 35^{\circ}$,则$\angle BCD$的度数为(
B
).
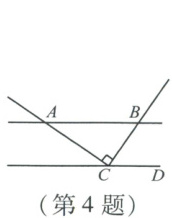
A.$65^{\circ}$
B.$55^{\circ}$
C.$45^{\circ}$
D.$35^{\circ}$
答案:B
解析:
∵AC⊥BC,∴∠ACB=90°。
在Rt△ABC中,∠BAC=35°,
∴∠ABC=90°-∠BAC=90°-35°=55°。
∵AB//CD,
∴∠BCD=∠ABC=55°(两直线平行,内错角相等)。
5. 若$a$,$b$,$c$为$\triangle ABC$的三边,且$a$,$b$满足$\sqrt{a - 3} + (b - 2)^2 = 0$,第三边$c$是整数,则$c$的值可以是(
B
).
A.1
B.3
C.5
D.7
答案:B
解析:
由$\sqrt{a - 3} + (b - 2)^2 = 0$,得$a-3=0$,$b-2=0$,所以$a=3$,$b=2$。根据三角形三边关系,$3-2 < c < 3+2$,即$1 < c < 5$。因为$c$是整数,所以$c=2,3,4$,选项中符合的是3。
6. 如图,若$\angle A = 70^{\circ}$,$\angle B = 40^{\circ}$,$\angle C = 32^{\circ}$,则$\angle BDC =$ (
C
).
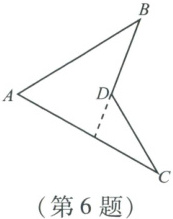
A.$102^{\circ}$
B.$110^{\circ}$
C.$142^{\circ}$
D.$148^{\circ}$
答案:C
解析:
连接AD并延长至点E。根据三角形外角性质,∠BDE=∠BAD+∠B,∠CDE=∠CAD+∠C。则∠BDC=∠BDE+∠CDE=∠BAD+∠B+∠CAD+∠C=(∠BAD+∠CAD)+∠B+∠C=∠A+∠B+∠C。已知∠A=70°,∠B=40°,∠C=32°,故∠BDC=70°+40°+32°=142°。
7. 已知一个等腰三角形的两条边长分别为$4 cm$和$6 cm$,则它的周长为(
C
).
A.$14 cm$
B.$16 cm$
C.$14 cm$或$16 cm$
D.不能确定
答案:C
解析:
若$4cm$为腰长,则三角形的三边长度分别为$4cm$,$4cm$,$6cm$,满足三角形三边关系(任意两边之和大于第三边),此时周长为 $4 + 4 + 6 = 14(cm)$。
若$6cm$为腰长,则三角形的三边长度分别为$6cm$,$6cm$,$4cm$,也满足三角形三边关系,此时周长为 $6 + 6 + 4 = 16(cm)$。
所以,等腰三角形的周长有两种可能,$14cm$或$16cm$。
8. 如图,$AD$,$BE$,$CF$是$\triangle ABC$的三条中线,则下列说法中错误的是(
C
).
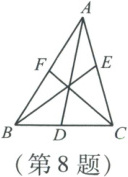
A.$AE = \frac{1}{2}AC$
B.$AB = 2BF$
C.$AD = CF$
D.$BD = DC$
答案:C
解析:
由题意知,$AD$、$BE$和$CF$是$\triangle ABC$的三条中线,
根据中线的性质,中线将对边分成两等份。
对于选项$AE = \frac{1}{2}AC$,因为$E$是$AC$的中点,所以该选项正确。
对于选项$AB = 2BF$,因为$F$是$AB$的中点,所以该选项正确。
对于选项$BD = DC$,因为$D$是$BC$的中点,所以该选项正确。
对于选项$AD = CF$,没有理由表明一条中线等于另一条中线,所以该选项错误。
9. 在$\triangle ABC$中,$\angle A=\angle C$,$CD$平分$\angle ACB$交$AB$于点$D$,$\angle ADC = 150^{\circ}$.设$\angle B$的度数为$x^{\circ}$,列方程可求得$\angle B$的度数为(
B
).
A.$150^{\circ}$
B.$140^{\circ}$
C.$130^{\circ}$
D.$120^{\circ}$
答案:B
解析:
设∠A=∠C=y°,∠B=x°。
∵△ABC内角和为180°,∴2y + x = 180°,即y=(180°-x)/2。
∵CD平分∠ACB,∴∠ACD=∠ACB/2=y/2。
在△ADC中,∠A + ∠ADC + ∠ACD=180°,∠ADC=150°,
∴y + 150° + y/2 = 180°,解得(3y)/2=30°,y=20°。
代入y=(180°-x)/2,得20°=(180°-x)/2,解得x=140°。





