
【题目】已知函数![]() ,
,![]() .
.
(![]() )求
)求![]() 的单调增区间.
的单调增区间.
(![]() )求
)求![]() 在
在![]() 的最大值,及此时
的最大值,及此时![]() 的取值.
的取值.
(![]() )若
)若![]() 为
为![]() 的一个零点,求
的一个零点,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 时,
时,![]() 取得最大值
取得最大值![]() ;(3)
;(3)![]() .
.
【解析】
试题(![]() )根据二倍角的正弦、余弦公式以及辅助角公式化简
)根据二倍角的正弦、余弦公式以及辅助角公式化简![]() ,解不等式
,解不等式![]() ,
,![]() ,即可得到
,即可得到![]() 的单调增区间;(
的单调增区间;(![]() )当
)当![]() 时,
时,![]() ,∴当
,∴当![]() 时,
时,![]() 取得最大值
取得最大值![]() ;(
;(![]() )由
)由![]() ,可得
,可得![]() ,结合
,结合![]() ,利用平方关系及两角和的正弦公式可得结果.
,利用平方关系及两角和的正弦公式可得结果.
试题解析:(![]() )
)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
令![]() ,
,![]() ,
,
得![]() ,
,![]() ,
,
∴![]() 的单调增区间为:
的单调增区间为:![]() ,
,![]() .
.
(![]() )当
)当![]() 时,
时,![]() ,
,
∴当![]() 时,即
时,即![]() 时,
时,
![]() 取得最大值
取得最大值![]() .
.
(![]() )若
)若![]() 为
为![]() 的一个零点,则
的一个零点,则![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]()
![]() .
.
【方法点晴】本题主要考查三角函数的单调性与最值以及三角函数恒等变换,属于难题.三角函数的图象与性质是高考考查的热点之一,经常考查定义域、值域、周期性、对称性、奇偶性、单调性、最值等,其中公式运用及其变形能力、运算能力、方程思想等可以在这些问题中进行体现,在复习时要注意基础知识的理解与落实.三角函数的性质由函数的解析式确定,在解答三角函数性质的综合试题时要抓住函数解析式这个关键,在函数解析式较为复杂时要注意使用三角恒等变换公式把函数解析式化为一个角的一个三角函数形式,然后利用正弦(余弦)函数的性质求解.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中, ![]() 是椭圆
是椭圆![]()
![]() 的右顶点,
的右顶点, ![]() 是上顶点,
是上顶点, ![]() 是椭圆位于第三象限上的任一点,连接
是椭圆位于第三象限上的任一点,连接![]() ,
, ![]() 分别交坐标轴于
分别交坐标轴于![]() ,
, ![]() 两点.
两点.
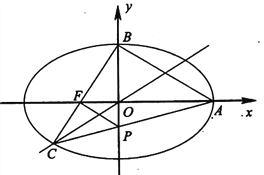
(1)若点![]() 为左焦点且直线
为左焦点且直线![]() 平分线段
平分线段![]() ,求椭圆的离心率;
,求椭圆的离心率;
(2)求证:四边形![]() 的面积是定值.
的面积是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列{an},a1=1,a2=2,对任意n∈N* , 有an+2=an , 数列{bn}满足bn+1﹣bn=an(n∈N*),若数列 ![]() 中的任意一项都在该数列中重复出现无数次,则满足要求的b1的值为
中的任意一项都在该数列中重复出现无数次,则满足要求的b1的值为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)=x2-x+b,且f(log2a)=b,log2f(a)=2(a>0且a≠1).
(1)求a,b的值;
(2)求f(log2x)的最小值及相应x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前项和为Sn , 若点An(n, ![]() )在函数f(x)=﹣x+c的图像上运动,其中c是与x无关的常数且a1=3.
)在函数f(x)=﹣x+c的图像上运动,其中c是与x无关的常数且a1=3.
(1)求数列{an}的通项公式;
(2)设bn=tanan+1tanan , tan195+tan3=atan2,求数列{bn}的前99项和(用含a的式子表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,则下列结论中正确结论的序号是__________.
,则下列结论中正确结论的序号是__________.
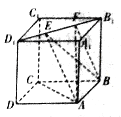
①![]() ;
;
②直线![]() 与平面
与平面![]() 所成角的正弦值为定值
所成角的正弦值为定值![]() ;
;
③当![]() 为定值,则三棱锥
为定值,则三棱锥![]() 的体积为定值;
的体积为定值;
④异面直线![]() 所成的角的余弦值为定值
所成的角的余弦值为定值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若学生![]() 一天学习数学超过两个小时的概率为
一天学习数学超过两个小时的概率为![]() (每天是相互独立没有影响的),一周内至少有四天每天学习数学超过两个小时,就说该生本周数学学习是投入的.
(每天是相互独立没有影响的),一周内至少有四天每天学习数学超过两个小时,就说该生本周数学学习是投入的.
(Ⅰ)①设学生![]() 本周一天学习数学超过两个小时的天数为
本周一天学习数学超过两个小时的天数为![]() 求
求![]() 的分布列与数学期望
的分布列与数学期望![]()
②求学生![]() 本周数学学习投入的概率.
本周数学学习投入的概率.
(Ⅱ)为了研究学生学习数学的投入程度和本周数学周练成绩的关系,随机在年级中抽取了![]() 名学生进行调查,所得数据如下表所示:
名学生进行调查,所得数据如下表所示:
成绩理想 | 成绩不太理想 | 合计 | |
数学学习投入 | 20 | 10 | 30 |
数学学习不太投入 | 10 | 15 | 25 |
合计 | 30 | 25 | 55 |
根据上述数据能否有![]() 的把握认为“学生学习数学的投入程度和本周数学成绩两事件有关”?
的把握认为“学生学习数学的投入程度和本周数学成绩两事件有关”?
附:![]()
|
|
|
|
|
|
|
|
|
|
| 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com