
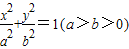 的两个焦点分别为F1(-c,0)和F2(c,0)(c>0),过点
的两个焦点分别为F1(-c,0)和F2(c,0)(c>0),过点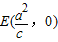 的直线与椭圆相交与A,B两点,且F1A∥F2B,|F1A|=2|F2B|.
的直线与椭圆相交与A,B两点,且F1A∥F2B,|F1A|=2|F2B|.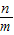 的值.
的值.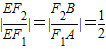 ,从而
,从而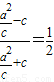 ,由此可以求出椭圆的离心率.
,由此可以求出椭圆的离心率.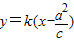 ,设A(x1,y1),B(x2,y2),
,设A(x1,y1),B(x2,y2),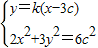 ,整理,得(2+3k2)x2-18k2cx+27k2c2-6c2=0.再由根的判别式和根与系数的关系求解.
,整理,得(2+3k2)x2-18k2cx+27k2c2-6c2=0.再由根的判别式和根与系数的关系求解.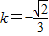 时,得
时,得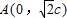 ,
,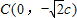 .线段AF1的垂直平分线l的方程为
.线段AF1的垂直平分线l的方程为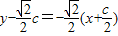 直线l与x轴的交点
直线l与x轴的交点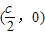 是△AF1C外接圆的圆心,因此外接圆的方程为
是△AF1C外接圆的圆心,因此外接圆的方程为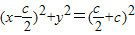 .由此可以推导出
.由此可以推导出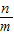 的值.
的值.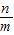 的值.
的值.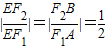 ,从而
,从而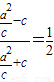
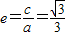
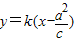 ,即y=k(x-3c).
,即y=k(x-3c).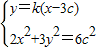
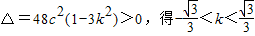
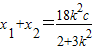 ①
①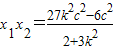 ②
②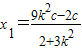 ,
,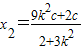
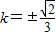 .
.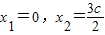
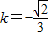 时,得
时,得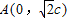 ,由已知得
,由已知得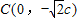 .
.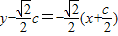 直线l与x轴
直线l与x轴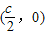 是△AF1C外接圆的圆心,
是△AF1C外接圆的圆心,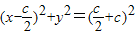 .
.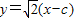 ,
,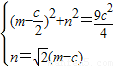 ,
,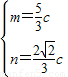 故
故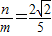
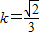 时,同理可得
时,同理可得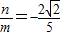 .
.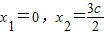
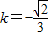 时,得
时,得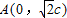 ,由已知得
,由已知得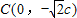
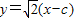 ,
,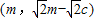 .
.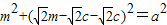 ,解得m=c(舍),或
,解得m=c(舍),或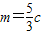 .
.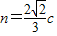 ,所以
,所以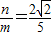 .当
.当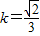 时同理可得
时同理可得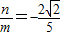


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(满分13分)
以知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,过点
,过点![]() 的直
的直
线与椭圆相交与![]() 两点,且
两点,且![]() 。
。
(1)求椭圆的离心率;w.w.w.k.s.5.u.c.o.m ![]()
(2)求直线AB的斜率;w.w.w.k.s.5.u.c.o.m ![]()
(3)设点C与点A关于坐标原点对称,直线![]() 上有一点
上有一点![]() 在
在![]()
![]() 的外接圆上,求
的外接圆上,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
以知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,过点
,过点![]() 的直线与椭圆相交与
的直线与椭圆相交与![]() 两点,且
两点,且![]() 。
。
(1) 求椭圆的离心率;
(2) 求直线AB的斜率;
(3) 设点C与点A关于坐标原点对称,直线![]() 上有一点
上有一点![]() 在
在![]()
![]() 的外接圆上,求
的外接圆上,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源:2011-2012年浙江省高二第一学期期中考试理科数学 题型:解答题
((本小题10分)
已知椭圆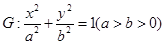 的两个焦点为
的两个焦点为 、
、 ,点
,点 在椭圆G上,且
在椭圆G上,且 ,且
,且 ,斜率为1的直线
,斜率为1的直线 与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
(1)求椭圆G的方程;
(2)求 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009天津卷理)(本小题满分14分)
以知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,过点
,过点![]() 的直线与椭圆相交与
的直线与椭圆相交与![]() 两点,且
两点,且![]() 。
。
(1) 求椭圆的离心率;
(2) 求直线AB的斜率;
(3) 设点C与点A关于坐标原点对称,直线![]() 上有一点
上有一点![]() 在
在![]()
![]() 的外接圆上,求
的外接圆上,求![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com