【题目】已知椭圆
的方程是
，双曲线
的左右焦点分别为的左右顶点，而的左右顶点分别是的左右焦点.
（1）求双曲线的方程；
（2）若直线
与双曲线恒有两个不同的交点，且
与的两个交点A和B满足
，求
的取值范围.
科目：高中数学 来源： 题型：
【题目】高三年级有500名学生，为了了解数学科的学习情况，现从中随机抽出若干名学生在一次测试中的数学成绩，制成如下频率分布表：
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
| 12 |
|
|
| |
| 4 |
|
|
| |
合计 |
|
根据上面图表，求
处的数值
在所给的坐标系中画出
的频率分布直方图；
根据题中信息估计总体平均数，并估计总体落在
中的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某厂销售部以箱为单位销售某种零件，每箱的定价为200元，低于100箱按原价销售；不低于100箱通过双方议价，买方能以优惠
成交的概率为0.6，以优惠
成交的概率为0.4.
（1）甲、乙两单位都要在该厂购买150箱这种零件，两单位各自达成的成交价相互独立，求甲单位优惠比例不低于乙单位优惠比例的概率；
（2）某单位需要这种零件650箱，求购买总价
的数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出下列四个命题：
若
为
的极值点，则
”的逆命题为真命题；
“平面向量
，
的夹角是钝角”的充分不必要条件是
；
若命题
，则 
；
命题“
，使得
”的否定是：“
，均有
”．其中不正确的个数是
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题：①设A，B为两个集合，则“
”是“
”的充分不必要条件；②
，
；③“
”是“
”的充要条件；④
，代数式
的值都是质数.其中的真命题是________.（填写序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，底面
是边长为2的菱形，
，
，平面
平面，点
为棱
的中点．
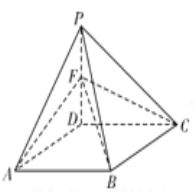
（Ⅰ）在棱
上是否存在一点
，使得
平面
，并说明理由；
（Ⅱ）当二面角
的余弦值为
时，求直线
与平面所成的角．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知在
中，
，
，点
在抛物线
上.
（1）求的边
所在的直线方程；
（2）求的面积最小值，并求出此时点的坐标；
（3）若
为线段上的任意一点，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系中，已知直线
的方程为
，
.
（1）若直线在
轴、
轴上的截距之和为-1，求坐标原点
到直线的距离；
（2）若直线与直线
：
和
：
分别相交于
、
两点，点
到、两点的距离相等，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】近年电子商务蓬勃发展， 
年某网购平台“双
”一天的销售业绩高达
亿元人民币，平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出
次成功交易，并对其评价进行统计，网购者对商品的满意率为
，对快递的满意率为
，其中对商品和快递都满意的交易为
次.
（1）根据已知条件完成下面的
列联表，并回答能否有
的把握认为“网购者对商品满意与对快递满意之间有关系”？
对快递满意 | 对快递不满意 | 合计 | |
对商品满意 |
| ||
对商品不满意 | |||
合计 |
|
（2）为进一步提高购物者的满意度，平台按分层抽样方法从中抽取
次交易进行问卷调查，详细了解满意与否的具体原因，并在这
次交易中再随机抽取
次进行电话回访，听取购物者意见.求电话回访的
次交易至少有一次对商品和快递都满意的概率.
附：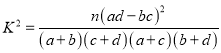 
（其中
为样本容量）
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
