
设数列 的前
的前 项和为
项和为 ,且
,且 ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(Ⅰ) (Ⅱ)
(Ⅱ)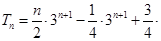
解析试题分析:(Ⅰ)由 可递推一个
可递推一个 .两式相减即可得到数列
.两式相减即可得到数列 的通项公式.在验证第一项是否符合即可.本小题的易错点是前n项和指的是
的通项公式.在验证第一项是否符合即可.本小题的易错点是前n项和指的是 .(Ⅱ)由第一步求出
.(Ⅱ)由第一步求出 再求出
再求出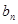 .根据所得的
.根据所得的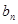 的通项式,是一个等差数列和一个等比数列相乘的形式.因此
的通项式,是一个等差数列和一个等比数列相乘的形式.因此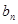 的前n项和利用错位相减法即可求得.本题属于数列的题型中较基础的题目,应用了解决数列的常用手段递推一项和错位相减法求数列的前n项和.但是计算不简单.
的前n项和利用错位相减法即可求得.本题属于数列的题型中较基础的题目,应用了解决数列的常用手段递推一项和错位相减法求数列的前n项和.但是计算不简单.
试题解析:(I)由题意得 =
= ①
①
 ②
②
①-②得
所以 4分
4分
经验证 时也满足上式,所以
时也满足上式,所以 6分
6分
(II) 由(1)得  ,
,
两式相减得 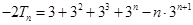 8分
8分 ,
,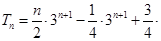 12分
12分
考点:1.数列递推思想.2.错位相减法求数列的前n项和.3.运算能力的培养.


科目:高中数学 来源: 题型:解答题
已知函数 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数.
(1)用 表示
表示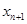 ;
;
(2) ,若
,若 ,试证明数列
,试证明数列 为等比数列,并求数列
为等比数列,并求数列 的通项公式;
的通项公式;
(3)若数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前 项和
项和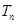 ,求
,求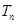 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com