练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆（a＞b＞0）的离心率，过点A（0，-b）和B（a，0）的直线与原点的距离为．

    （1）求椭圆的方程．

    （2）已知定点E（-1，0），若直线y＝kx＋2（k≠0）与椭圆交于C、D两点．问：是否存在k的值，使以CD为直径的圆过E点?请说明理由．

    【答案】（1）；（2）存在

    【解析】

    试题分析：（1）直线方程为： 椭圆方程为 ；（2）假若存在这样的值，由．

    ．要使以为直径的圆过点当且仅当时

    存在，使得以为直径的圆过点．

    试题解析：（1）直线方程为：．

    依题意 解得

    ∴ 椭圆方程为

    （2）假若存在这样的值，由得．

    ． ①

    设，、，，则 ②

    而．

    要使以为直径的圆过点，当且仅当时，则，即．

    ． ③

    将②式代入③整理解得．经验证，，使①成立．

    综上可知，存在，使得以为直径的圆过点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B={抽到二等品},事件C={抽到三等品},且已知P(A)=0.65,P(B)=0.2,P(C)=0.1.则事件“抽到的是二等品或三等品”的概率为(　　)

    A. 0.7 B. 0.65

    C. 0.35 D. 0.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知以点为圆心的圆过原点.

    （1）设直线与圆交于点，若，求圆的方程；

    （2）在（1）的条件下，设，且分别是直线和圆上的动点，求的最大值及此时点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（，，）．

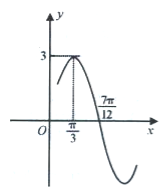
    （1）若的部分图像如图所示，求的解析式；

    （2）在（1）的条件下，求最小正实数，使得函数的图象向左平移个单位后所对应的函数是偶函数；

    （3）若在上是单调递增函数，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某班主任对全班50名学生作了一次调查，所得数据如表：


    认为作业多

    认为作业不多

    总计

    喜欢玩电脑游戏

    18

    9

    27

    不喜欢玩电脑游戏

    8

    15

    23

    总计

    26

    24

    50

    由表中数据计算得到K2的观测值k≈5.059，于是________（填“能”或“不能”）在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数()是偶函数．

    （1）求k的值；

    （2）若函数的图象与直线没有交点，求的取值范围；

    （3）若函数，，是否存在实数使得最小值为，若存在，求出的值; 若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)在某一个周期内的图象时,列表并填入了部分数据,如表:

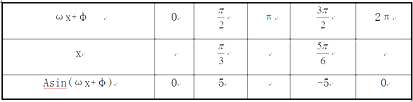
    (1)请将上表数据补充完整,并直接写出函数f(x)的解析式.

    (2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为,求θ的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了判断高中三年级学生选修文理科是否与性别有关，现随机抽取50名学生，得到2×2列联表：

    理科

    文科

    总计

    男

    13

    10

    23

    女

    7

    20

    27

    总计

    20

    30

    50

    已知P(K2≥3.841)≈0.05，P(K2≥5.024)≈0.025.根据表中数据，得到K2≈4.844，则认为选修文理科与性别有关系出错的可能性约为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为，P为椭圆C上任意一点，且最小值为0.

    （1）求曲线C的方程；

    （2）若动直线均与椭圆C相切，且，试探究在x轴上是否存在定点B，使得点B到的距离之积恒为1？若存在，请求出点B的坐标；若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案