
已知![]() ,函数
,函数![]() ,
,![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(2)是否存在实数![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直? 若存在,求出
轴垂直? 若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上无最小值;
上无最小值;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
(2) 不存在![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直
轴垂直
(1)解:∵![]() ,∴
,∴![]() .
.
令![]() ,得
,得![]() .
.
①若![]() ,则
,则![]() ,
,![]() 在区间
在区间![]() 上单调递增,此时函数
上单调递增,此时函数![]() 无最小值.
无最小值.
②若![]() ,当
,当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() .
.
③若![]() ,则
,则![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() .
.
综上可知,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上无最小值;
上无最小值;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
(2)解:∵![]() ,
,![]() ,
,
∴ ![]()
![]() .
.
由(1)可知,当![]() 时,
时,![]() .
.
此时![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,即
,即![]() .
.
当![]() ,
,![]() ,
,![]() ,
,
∴ .
.
曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直等价于方程
轴垂直等价于方程![]() 有实数解.
有实数解.
而![]() ,即方程
,即方程![]() 无实数解.
无实数解.
故不存在![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直.
轴垂直.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:2012届浙江省宁波万里国际学校高三上期中理科数学试卷(解析版) 题型:解答题
(本题满分14分)已知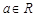 ,函数
,函数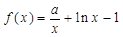 ,
,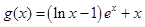 (其中
(其中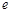 为自然对数的底数).
为自然对数的底数).
(Ⅰ)判断函数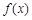 在
在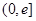 上的单调性;
上的单调性;
(II)是否存在实数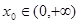 ,使曲线
,使曲线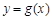 在点
在点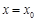 处的切线与
处的切线与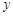 轴垂直? 若存在,
轴垂直? 若存在,
求出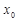 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)若实数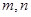 满足
满足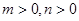 ,求证:
,求证: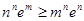 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年黑龙江省高三上学期期末考试文科数学试卷 题型:解答题
已知 ,函数
,函数 ,(其中
,(其中 为自然对数的底数).
为自然对数的底数).
(1)判断函数 在
在 上的单调性;
上的单调性;
(2)是否存在实数 ,使曲线
,使曲线 在点
在点 处的切线与
处的切线与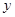 轴垂直? 若存在,求出
轴垂直? 若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第七次月考理科数学 题型:解答题
已知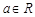 ,函数
,函数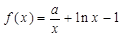 ,
,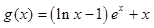 (其中
(其中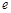 为自然对数的底数).(1)判断函数
为自然对数的底数).(1)判断函数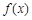 在
在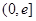 上的单调性;
上的单调性;
(2)是否存在实数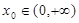 ,使曲线
,使曲线 在点
在点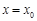 处的切线与
处的切线与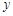 轴垂直? 若存在,
轴垂直? 若存在,
求出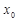 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若实数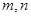 满足
满足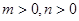 ,求证:
,求证: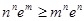 。
。
查看答案和解析>>
科目:高中数学 来源:河北省2010年高考适应性测试数学试卷理 题型:解答题
已知 ,函数
,函数 ,
, (其中
(其中 为自然对数的底数).(1)判断函数
为自然对数的底数).(1)判断函数 在区间
在区间 上的单调性;(2)是否存在实数
上的单调性;(2)是否存在实数 ,使曲线
,使曲线 在点
在点 处的切线与
处的切线与 轴垂直? 若存在,求出
轴垂直? 若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com