
【题目】如图,AC是圆O的直径,点B在圆O上, ![]() ,
, ![]() 交
交![]() 于
于![]() ,
, ![]()
(1)证明: ![]() ;
;
(2) 求平面![]() 与
与![]() 所成的锐角二面角的余弦值.
所成的锐角二面角的余弦值.

【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)先利用线面垂直的性质和判定得到线线垂直和线面垂直,再根据直径所对的圆周角为直角和线面垂直的性质、等腰直角三角形得到线线垂直,进而利用线面垂直的判定定理进行证明;(2)根据垂直关系建立适当的空间直角坐标系,写出相关点坐标,求出有关平面的法向量,再利用有关公式进行求解 .
试题解析:(1)证明:∵EA⊥平面ABC,BM![]() 平面ABC,∴EA⊥BM.
平面ABC,∴EA⊥BM.
又∵BM⊥AC,EA∩AC=A,∴BM⊥平面ACFE,
而EM![]() 平面ACFE,∴BM⊥EM.∵AC是圆O的直径,∴∠ABC=90°.
平面ACFE,∴BM⊥EM.∵AC是圆O的直径,∴∠ABC=90°.
又∵∠BAC=30°,AC=4,∴AB=![]() ,BC=2,AM=3,CM=1.
,BC=2,AM=3,CM=1.
∵EA⊥平面ABC,FC‖EA, ![]() ∴FC⊥平面ABCD.
∴FC⊥平面ABCD.
∴△EAM与△FCM都是等腰直角三角形.
∴∠EMA=∠FMC=45°.∴∠EMF=90°,即EM⊥MF(也可由勾股定理证得).
∵MF∩BM=M,∴EM⊥平面MBF.
而BF![]() 平面MBF,∴EM⊥BF.
平面MBF,∴EM⊥BF.
(2)解法一:延长EF交AC于G,连BG,过C作CH⊥BG,连接FH.
由(1)知FC⊥平面ABC,BG![]() 平面ABC,∴FC⊥BG.
平面ABC,∴FC⊥BG.
而FC∩CH=C,∴BG⊥平面FCH.∵FH平面FCH,∴FH⊥BG,
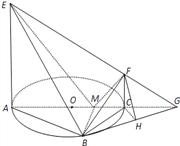
∴∠FHC为平面BEF与平面ABC所成的二面角的平面角.
在Rt△ABC中,∵∠BAC=30°,AC=4,
∴BM=ABsin![]() =
=![]() .
.
由![]() .
.
∵![]() 与
与![]() 相似,
相似, ![]() ,
, ![]()
∴△FCH是等腰直角三角形,∠FHCspan>=45°.∴平面BEF与平面ABC所成的锐二面角的余弦值为![]()
解法二:如图:以A为坐标原点,AC、AE分别为y轴和Z轴建立空间直角坐标系,
由已知得![]() ,
, ![]() ,
,
![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
由![]()
![]() 得
得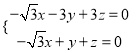
令![]() ,由
,由![]() 得平面ABC的一个法向量为
得平面ABC的一个法向量为![]()
设平面![]() 与
与![]() 所成的锐角二面角为
所成的锐角二面角为![]() ,
,
则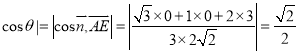
所以,平面BEF与平面ABC所成的锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() ,(x∈(﹣∞,0]∪[2,+∞))的值域为( )
,(x∈(﹣∞,0]∪[2,+∞))的值域为( )
A.[0,4]
B.[0,2)∪(2,4]
C.(﹣∞,0]∪[4,+∞)
D.(﹣∞,2)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,其中函数
,其中函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(1)确定![]() 与
与![]() 的关系;若
的关系;若![]() ,并试讨论函数
,并试讨论函数![]() 的单调性;
的单调性;
(2)设斜率为![]() 的直线与函数
的直线与函数![]() 的图象交于两点
的图象交于两点![]()
![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 为参数
为参数![]() 和直线
和直线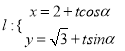
![]() 其中
其中![]() 为参数,
为参数, ![]() 为直线
为直线![]() 的倾斜角
的倾斜角![]() .
.
(1)当![]() 时,求圆上的点到直线
时,求圆上的点到直线![]() 的距离的最小值;
的距离的最小值;
(2)当直线![]() 与圆
与圆![]() 有公共点时,求
有公共点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线
轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线![]() 的参数方程为
的参数方程为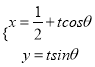 ,(
,( ![]() 为参数,
为参数, ![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(0,2),斜率为k,圆Q:x2+y2﹣12x+32=0.
(1)若直线l和圆相切,求直线l的方程;
(2)若直线l和圆交于A、B两个不同的点,问是否存在常数k,使得![]() +
+![]() 与
与![]() 共线?若存在,求出k的值;若不存在,请说明理由.
共线?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线![]()
![]() 上有一点
上有一点![]() (
(![]() ),点
),点![]() 在
在![]() 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线![]() 的右焦点,过点
的右焦点,过点![]() 作双曲线
作双曲线![]() 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为![]() ,
, ![]() ,若平行四边形
,若平行四边形![]() 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com