
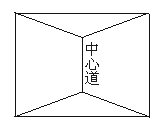
(1)若道路网的总长度不超过5.5 km,试求中心道的取值范围;
(2)问中心道长为何值时,道路网的总长度最短?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009安徽卷理)(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区.B肯定是受A感染的.对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是![]() .同样也假定D受A、B和C感染的概率都是
.同样也假定D受A、B和C感染的概率都是![]() .在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量.写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量.写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区。B肯定是受A感染的。对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是![]() 。同样也假定D受A、B和C感染的概率都是
。同样也假定D受A、B和C感染的概率都是![]() 。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
查看答案和解析>>
科目:高中数学 来源:2009年普通高等学校招生全国统一考试理科数学(安徽卷) 题型:解答题
(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区。B肯定是受A感染的。对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是 。同样也假定D受A、B和C感染的概率都是
。同样也假定D受A、B和C感染的概率都是 。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com