
请你根据公理
2及三个推论,解决以下问题:(1)
不共面的四点可以确定几个平面?(2)
三条直线两两平行但不共面,它们可以确定几个平面?(3)
共点的三条直线可以确定几个平面?|
解: (1)由于四个点不共面,可知任意三个点不共线.由公理2,任何不在同一直线上三个点都确定一个平面.如图所示可知,共确定4个平面,分别是平面ABC,平面ABD,平面ACD,平面BCD.
(2)由推论3可知,两条平行直线确定一个平面,若另一条直线在该平面内,则三条平行线只确定一个平面;若另一条直线不在该平面内,则每两条平行线都可以确定一个平面.如图,三条平行线a、b、c确定的三个平面分别为α、β、γ.三棱柱的三条侧棱便符合这一条件.
∴由条件可知,它们可以确定三个平面. (3) 已知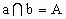 ,可知a,b确定一个平面,设为α.给出第三条直线l,由于三条直线相交于同一点,则 ,可知a,b确定一个平面,设为α.给出第三条直线l,由于三条直线相交于同一点,则若 l上另有一点BÎ α,则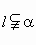 ,此时a、b、l都在平面α内,如下图. ,此时a、b、l都在平面α内,如下图.
若l上有一点B
∵ 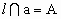 ,可知l,a确定一个平面. ,可知l,a确定一个平面.
综上所述,共点的三条直线可以确定 1个或3个平面. |
|
“确定”和“有且只有”是同义词,也就是说“确定一个平面”指“存在”和“唯一”两个方面.只要满足公理2和推论中的条件,便可确定平面. |


科目:高中数学 来源:数学教研室 题型:044
请你根据公理2及三个推论,解决以下问题:
(1)不共面的四点可以确定几个平面?
(2)三条直线两两平行但不共面,它们可以确定几个平面?
(3)共点的三条直线可以确定几个平面?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com