Question

【题目】设函数f（x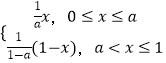）= ，a为常数，且a∈（0，1）．
（1）若x0满足f（x0）=x0 ， 则称x0为f（x）的一阶周期点，证明函数f（x）有且只有两个一阶周期点；
（2）若x0满足f（f（x0））=x0 ， 且f（x0）≠x0 ， 则称x0为f（x）的二阶周期点，当a= 时，求函数f（x）的二阶周期点．

Answer 1

【答案】
（1）证明：由题可得，当0≤x≤a时， ，因为a∈（0，1），所以x=0；

当a＜x≤1时， ，因为a∈（0，1），所以x= ，

所以函数f（x）有且只有两个一阶周期点．

（2）解：当 时，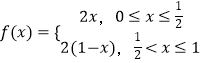

所以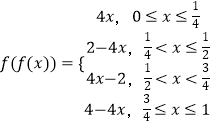

当 时，由4x=x，解得x=0，

因为f（0）=0，故x=0不是f（x）的二阶周期点；

当 时，由2﹣4x=x，解得 ，

因为 ，故 是f（x）的二阶周期点；

当 时，由4x﹣2=x，解得 ，

因为 ，故 不是f（x）的二阶周期点；

当 时，由4﹣4x=x，解得 ，

因为 ，故 是f（x）的二阶周期点；

综上，当 时，函数f（x）的二阶周期点为x1= ，x2= ．

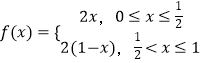【解析】（1）利用定义通过当0≤x≤a时，当a＜x≤1时，验证函数f（x）有且只有两个一阶周期点．（2）当 时， ，推出 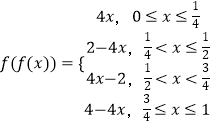，利用函数的定义域，通过分段求解即可．