
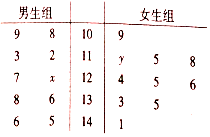
 ��ijСѧ�������ʴ���˶����ϣ���10��������10��Ů����һ���������Ĵ�������ͳ�ƣ��õ�������ʾ��Ҷͼ��
��ijСѧ�������ʴ���˶����ϣ���10��������10��Ů����һ���������Ĵ�������ͳ�ƣ��õ�������ʾ��Ҷͼ������ ��1������120+$\frac{7+x}{2}$=125�����x������ƽ�����ļ��㹫ʽ�ɵ�y��
��2����Ϊһ��������������������115�Ҳ�����125��ѧ���У�����ֻ��1�ˣ�Ů��ֻ��4�ˣ�����������ѡ�ϵĸ���Ϊ$\frac{1}{10}$��Ů����ѡ�ϵĸ���Ϊ$\frac{4}{10}$��X����ȡֵΪ0��1��2������������뻥���¼��ĸ��ʼ��㹫ʽ���ɵó���
��� �⣺��1����120+$\frac{7+x}{2}$=125�����x=3��
��$\frac{100+110��3+120��3+140+9+y+5+8+4+5+6+3+5+1}{10}$=124�����y=4��
��2����Ϊһ��������������������115�Ҳ�����125��ѧ���У�����ֻ��1�ˣ�Ů��ֻ��4�ˣ�
����������ѡ�ϵĸ���Ϊ$\frac{1}{10}$��Ů����ѡ�ϵĸ���Ϊ$\frac{4}{10}$��X����ȡֵΪ0��1��2��
��P��X=0��=$\frac{9}{10}��\frac{6}{10}$=$\frac{54}{100}$��P��X=1��=$\frac{1}{10}��\frac{6}{10}+\frac{9}{10}��\frac{4}{10}$=$\frac{42}{100}$��P��X=2��=$\frac{1}{10}��\frac{4}{10}$=$\frac{4}{100}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{54}{100}$ | $\frac{42}{100}$ | $\frac{4}{100}$ |
���� ���⿼���˾�Ҷͼ�����ʡ���λ����ƽ�����ļ��㹫ʽ��������뻥���¼��ĸ��ʼ��㹫ʽ����������ķֲ�������ѧ������������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{3}+1}}{4}$ | B�� | $\frac{{\sqrt{3}-1}}{2}$ | C�� | $\frac{{3-\sqrt{3}}}{4}$ | D�� | $\frac{{3-\sqrt{3}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��-1 | B�� | a��-1 | C�� | a��1 | D�� | a��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{26}{5}$ | B�� | -$\frac{26}{5}$ | C�� | ��$\frac{26}{5}$ | D�� | -$\frac{5}{26}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | -3 | C�� | $\frac{3}{2}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{4}{5}+\frac{3}{5}i$ | B�� | $-\frac{4}{5}-\frac{3}{5}i$ | C�� | $-\frac{4}{25}+\frac{3}{25}i$ | D�� | $-\frac{4}{25}-\frac{3}{25}i$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com