
(本题满分12分)
已知函数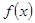 的定义域是
的定义域是 ,且满足
,且满足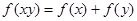 ,
,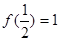 ,如果对于0<x<y,都有
,如果对于0<x<y,都有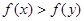 ,
,
(1)求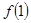 ;
;
(2)解不等式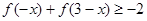
科目:高中数学 来源: 题型:解答题
某医药研究所开发一种新药,在实验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量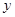 (微克)与时间
(微克)与时间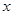 (小时)之间满足
(小时)之间满足 ,
,
其对应曲线(如图所示)过点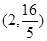 .
.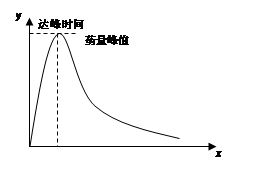
(1)试求药量峰值(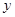 的最大值)与达峰时间(
的最大值)与达峰时间(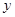 取最大值时对应的
取最大值时对应的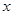 值);
值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间?(精确到0.01小时)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)设函数
 满足:
满足: 都有
都有 ,且
,且 时,
时, 取极小值
取极小值
(1) 的解析式;
的解析式;
(2)当 时,证明:函数图象上任意两点处的切线不可能互相垂直;
时,证明:函数图象上任意两点处的切线不可能互相垂直;
(3)设 , 当
, 当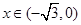 时,求函数
时,求函数 的最小值,并指出当
的最小值,并指出当 取最小值时相应的
取最小值时相应的 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知二次函数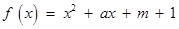 ,关于
,关于 的不等式
的不等式 的解集为
的解集为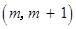 ,其中
,其中 为非零常数.设
为非零常数.设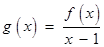 .
.
(1)求 的值;
的值;
(2)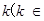 R
R 如何取值时,函数
如何取值时,函数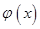
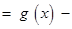
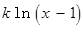 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若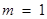 ,且
,且
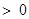 ,求证:
,求证: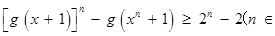 N
N
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)设计一副宣传画,要求画面积为4840 ,画面的宽与高的比为
,画面的宽与高的比为 ,画面的上,下各留8
,画面的上,下各留8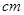 空白,左右各留5
空白,左右各留5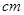 空白,怎样确定画面的高于宽尺寸,能使宣传画所用纸张面积最小?
空白,怎样确定画面的高于宽尺寸,能使宣传画所用纸张面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)某企业拟投资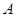 、
、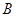 两个项目,预计投资
两个项目,预计投资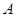 项目
项目 万元可获得利润
万元可获得利润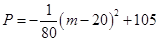
万元;投资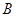 项目
项目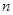 万元可获得利润
万元可获得利润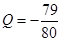
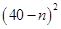
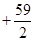
 万元.若该企业用40
万元.若该企业用40
万元来投资这两个项目,则分别投资多少万元能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
(本小题满分12分)某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为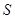 平方米.
平方米.
(1)分别写出用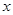 表示
表示 和用
和用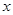 表示
表示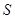 的函数关系式(写出函数定义域);
的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com