
(��)��x��[0��1]ʱ������f(x)�Ľ���ʽ��
(��)������l�ķ��̣�
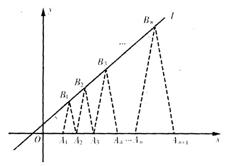
(��)����B1(b1��2)��B2(b2��3)������Bn(bn��n+1)��l�ϣ�A1(x1��0)��A2(x2��0)������An(xn��0)����Ϊx���ϵĵ㣬��ͼ����n��N*����An��Bn��An+1������AnAn+1Ϊ�ױߵĵ��������Σ���x1=a(0��a��1)��������{xn}�ǵȲ����У���a��ֵ������{xn}��ͨ�ʽ��
�𰸣��⣺(��)��0��x��1ʱ����-1��-x��0��
��f(-x)=-t(-x)3+t��(-x)��
��f(-x)=f(x)��
��f(x)=tx3-tx��x��[0��1]��
��f��(x)=3tx2-t������f��(![]() )=1����t=-4��
)=1����t=-4��
��f(x)=-4x3+4x(x��[0��1])��
(��)�������е�Ϊ(![]() ��f(
��f(![]() ))��(
))��(![]() ��
��![]() )��l��б��Ϊk1=f��(
)��l��б��Ϊk1=f��(![]() )=1��
)=1��
��ֱ�ߵ�бʽ����֪l�ķ���Ϊy=x+1��
(��)�ߵ�Bn(bn��n+1)��ֱ��y=x+1�ϣ�
��bn=n��
��![]() =n����xn+xn+1=2n��
=n����xn+xn+1=2n��
�ɴ��У�xn+1+xn+2=2n+2��
��ʽ����ã�xn+2-xn=2��
������{xn}���������������ż����ֱ���2Ϊ����ĵȲ����У�
��x1+x2=2��x1=a����x2=2-a��
��x2n-1=x1+2(n-1)=(2n-1)+a-1��
x2n=x2+2(n-1)=2-a+2n-2=2n-a��

���ҽ���a-1=-a��a=![]() ʱ��{xn}Ϊ�Ȳ����У�
ʱ��{xn}Ϊ�Ȳ����У�
��ʱ����{xn}��ͨ�ʽΪxn=n-![]() ��
��
(��)���⣺ͬǰ��xn+1+xn=2n����xn+1=-xn+2n��
��xn+1+p(n+1)+q=-(xn+pn+q)��
չ���ã�xn+1=-xn-2pn-2q-p��
�Ƚϵ�![]() �����p=-1��q=
�����p=-1��q=![]() ��
��
��xn+1-(n+1)+![]() =-(xn-n+
=-(xn-n+![]() )��
)��
��bn=xn-n+![]() ������ʽΪbn+1=-bn��
������ʽΪbn+1=-bn��
��{bn}����-1Ϊ���ȣ�����Ϊb1=x1-1+![]() =a-
=a-![]() �ĵȱ�����.
�ĵȱ�����.
��bn=(a-![]() )(-1)n��
)(-1)n��
��xn-n+![]() =(a-
=(a-![]() )(-1)n��
)(-1)n��
��xn=(a-![]() )(-1)n+n-
)(-1)n+n-![]() ��
��
��{xn}�ǵȲ����У�![]()
��a-![]() =0����a=
=0����a=![]() ��
��
��ʱ��xn=n-![]() ��
��


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 | x+b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ͬ���� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����С������12�֣�
�躯��f(x)=ax+![]() (a,b��Z)������y=f(x)�ڵ㣨2��f(2)���������߷���Ϊy=3��
(a,b��Z)������y=f(x)�ڵ㣨2��f(2)���������߷���Ϊy=3��
������f(x)�Ľ���ʽ��
����֤��������y=f(x)��ͼ����һ�����ĶԳ�ͼ�Σ�������Գ����ģ�
����֤��������y=f(x)����һ���������ֱ��x=1��ֱ��y=x��Χ�����ε����Ϊ��ֵ��������˶�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����С������12�֣�
�躯��f(x)=ax+![]() (a,b��Z)������y=f(x)�ڵ㣨2��f(2)���������߷���Ϊy=3��
(a,b��Z)������y=f(x)�ڵ㣨2��f(2)���������߷���Ϊy=3��
������f(x)�Ľ���ʽ��
����֤��������y=f(x)��ͼ����һ�����ĶԳ�ͼ�Σ�������Գ����ģ�
����֤��������y=f(x)����һ���������ֱ��x=1��ֱ��y=x��Χ�����ε����Ϊ��ֵ��������˶�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����С������14�֣���ͼ9-3����֪������OAΪy=kx(k>0��x>0)������OBΪy= ��kx(x>0)������P(x��y)�ڡ�AOx���ڲ���PM��OA��M��PN��OB��N���ı���ONPM�����ǡΪk.
��1����kΪ��ֵʱ������P��������y�Ǻ�����x�ĺ��������������y=f(x)�Ľ���ʽ��
 ��2������k��ȡֵ��Χ��ȷ��y=f(x)�Ķ�����.
��2������k��ȡֵ��Χ��ȷ��y=f(x)�Ķ�����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com