
已知函数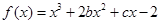 的图象在与
的图象在与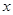 轴交点处的切线方程是
轴交点处的切线方程是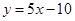 .
.
(I)求函数 的解析式;
的解析式;
(II)设函数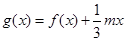 ,若
,若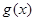 的极值存在,求实数
的极值存在,求实数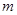 的取值范围以及函数
的取值范围以及函数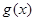 取得极值时对应的自变量
取得极值时对应的自变量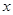 的值.
的值.
(I)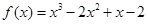 ;(II)
;(II) 时,函数
时,函数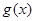 有极值;
有极值;
当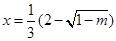 时,
时,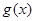 有极大值;当
有极大值;当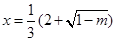 时,
时,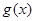 有极小值.
有极小值.
【解析】
试题分析:( I)涉及切线,便要求出切点.本题中切点如何求?函数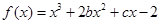 的图象在与
的图象在与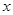 轴交点处的切线方程是
轴交点处的切线方程是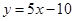 .说明切点就是直线
.说明切点就是直线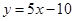 与
与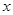 轴交点,所以令
轴交点,所以令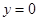 便得切点为(2,0).切点既在切线上又曲线,所以有
便得切点为(2,0).切点既在切线上又曲线,所以有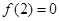 , 即
, 即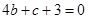 .
.
函数在切点处的导数就是切线的斜率,所以由已知有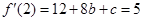 即
即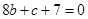 .这样便得一个方程组,解这个方程组求出
.这样便得一个方程组,解这个方程组求出 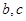 便
便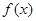 的解析式.
的解析式.
(II)将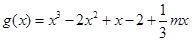 求导得,
求导得,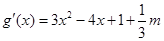 ,
,
令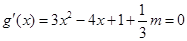 .这是一个二次方程,要使得函数有极值,则方程要有两个不同的实数根,所以
.这是一个二次方程,要使得函数有极值,则方程要有两个不同的实数根,所以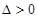 ,由此可得
,由此可得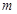 的范围.解方程
的范围.解方程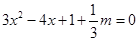 有便得取得极值时
有便得取得极值时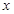 的值.
的值.
试题解析:( I)由已知,切点为(2,0), 故有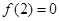 , 即
, 即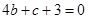
又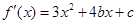 ,由已知
,由已知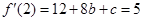 得
得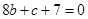
联立①②,解得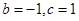 .所以函数的解析式为
.所以函数的解析式为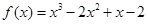
(II)因为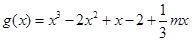
令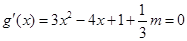
当函数有极值时,则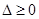 ,方程
,方程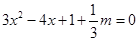 有实数解,
由
有实数解,
由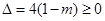 ,得
,得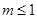 .
.
①当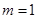 时,
时,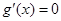 有实数
有实数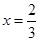 ,在
,在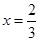 左右两侧均有
左右两侧均有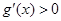 ,故函数
,故函数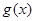 无极值
无极值
②当m<1时,g'(x)=0有两个实数根x1=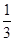 (2
(2
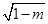 ),
x2=
),
x2=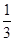 (2+
(2+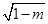 ),
g(x),g'(x) 的情况如下表:
),
g(x),g'(x) 的情况如下表:
|
|
|
|
|
|
|
|
|
+ |
0 |
|
0 |
+ |
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以在 时,函数
时,函数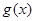 有极值;
有极值;
当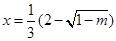 时,
时,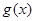 有极大值;当
有极大值;当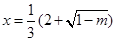 时,
时,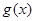 有极小值.
有极小值.
考点:导数的应用.


科目:高中数学 来源: 题型:
已知函数![]() 的图象在与
的图象在与![]() 轴交点处的切线方程是
轴交点处的切线方程是![]() 。
。
(I)求函数![]() 的解析式;
的解析式;
(II)设函数![]() ,若
,若![]() 的极值存在,求实数
的极值存在,求实数![]() 的取值范围以及函数
的取值范围以及函数![]() 取得极值时对应的自变量
取得极值时对应的自变量![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
已知函数![]() 的图象在与
的图象在与![]() 轴交点处的切线方程是
轴交点处的切线方程是![]() 。
。
(1)求函数![]() 的解析式;
的解析式;
(2)设函数![]() ,若
,若![]() 的极值存在,求实数
的极值存在,求实数![]() 的取值范围以及函数
的取值范围以及函数![]() 取得极值时对应的自变量
取得极值时对应的自变量![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2014届山东省淄博市高二下学期期中模块检测文科数学试卷(解析版) 题型:解答题
已知函数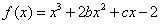 的图象在与
的图象在与 轴交点处的切线方程是
轴交点处的切线方程是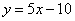 .
.
(Ⅰ)求函数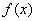 的解析式;
的解析式;
(Ⅱ)设函数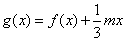 ,若
,若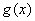 的极值存在,求实数
的极值存在,求实数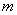 的取值范围以及当
的取值范围以及当 取何值时函数
取何值时函数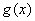 分别取得极大和极小值.
分别取得极大和极小值.
查看答案和解析>>
科目:高中数学 来源:2010届高三数学每周精析精练:函数 题型:解答题
已知函数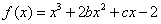 的图象在与
的图象在与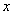 轴交点处的切线方程是
轴交点处的切线方程是 。
。
(I)求函数 的解析式;
的解析式;
(II)设函数 ,若
,若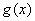 的极值存在,求实数
的极值存在,求实数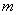 的取值范围以及函数
的取值范围以及函数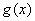 取得极值时对应的自变量
取得极值时对应的自变量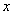 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com