
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 、
、![]() ,
,![]() ,点
,点![]() 在椭圆上,且
在椭圆上,且![]() 的周长为
的周长为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 的坐标为
的坐标为![]() ,不过原点
,不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,
,![]() ,
,![]() 三点共线,求
三点共线,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)根据焦距和焦点三角形周长可求得![]() ,利用
,利用![]() 求得
求得![]() ,从而可得椭圆的方程;(Ⅱ)当直线
,从而可得椭圆的方程;(Ⅱ)当直线![]() 斜率不存在时,可判断出
斜率不存在时,可判断出![]() ,
,![]() ,
,![]() 三点不共线,不符合题意;所以可假设出直线方程,与椭圆方程联立,利用韦达定理表示出
三点不共线,不符合题意;所以可假设出直线方程,与椭圆方程联立,利用韦达定理表示出![]() 和
和![]() ;由三点共线得到斜率相等关系,从而可求得
;由三点共线得到斜率相等关系,从而可求得![]() ;利用弦长公式和点到直线距离公式求得
;利用弦长公式和点到直线距离公式求得![]() 和
和![]() ,代入可整理出:
,代入可整理出: ,可知当
,可知当![]() 时取最大值.
时取最大值.
(Ⅰ)由题意得:![]() ,
,![]()
解得:![]() ,
,![]()
![]()
![]() 椭圆
椭圆![]() 的方程为
的方程为![]()
(Ⅱ)设![]() ,
,![]()
当直线![]() 与
与![]() 轴垂直时,由椭圆的对称性可知,点
轴垂直时,由椭圆的对称性可知,点![]() 在
在![]() 轴上,且与
轴上,且与![]() 点不重合
点不重合
显然![]() ,
,![]() ,
,![]() 三点不共线,不符合题设条件
三点不共线,不符合题设条件
故可设直线![]() 的方程
的方程![]()
由![]() ,消去
,消去![]() 整理得:
整理得:![]() ……①
……①
则![]()
![]() ,
,![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
![]() ,
,![]() ,
,![]() 三点共线
三点共线 ![]()

![]()
![]()
此时方程①为:![]() ,则
,则![]()
![]()
则![]() ,
,![]()
![]()
又![]()
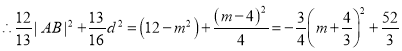
![]() 当
当![]() 时,
时,![]() 的最大值为
的最大值为![]()


科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,点O是四边形ABCD的中心,关于直线A1O,下列说法正确的是( )
A. A1O∥DCB. A1O⊥BCC. A1O∥平面BCDD. A1O⊥平面ABD
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 、
、![]() ,
,![]() ,点
,点![]() 在椭圆上,且
在椭圆上,且![]() 的周长为
的周长为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 的坐标为
的坐标为![]() ,不过原点
,不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,
,![]() ,
,![]() 三点共线,求
三点共线,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?如果存在,求
?如果存在,求![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十三届全国人大二次会议于2019年3月5日在京召开.为了了解某校大学生对两会的关注程度,学校媒体在开幕后的第二天,从学生中随机抽取了180人,对是否收看2019年两会开幕会情况进行了问卷调查,统计数据得到列联表如下:
收看 | 没收看 | 合计 | |
男生 | 40 | ||
女生 | 30 | 60 | |
合计 |
(1)请完成列联表;
(2)根据上表说明,能否有99%的把握认为该校大学生收看开幕会与性别有关?(结果精确到0.001)
附: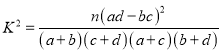 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A'B'C',AC=2,BC=4,∠ACB=120°,∠ACC'=90°,且平面AB'C⊥平面ABC,二面角A'﹣AC﹣B'为30°,E、F分别为A'C、B'C'的中点.

(1)求证:EF∥平面AB'C;
(2)求B'到平面ABC的距离;
(3)求二面角A﹣BB'﹣C'的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com