
【题目】已知![]() ,
, ![]() .
.
(1)求![]() 在点
在点![]() 处的切线;
处的切线;
(2)讨论![]() 的单调性;
的单调性;
(3)当![]() ,
, ![]() 时,求证:
时,求证: ![]() .
.
【答案】(1)![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】试题分析:(1)求出原函数的导函数,求出在![]() 处的导数值,即为切线斜率,代入直线方程的点斜式求得切线方程;
处的导数值,即为切线斜率,代入直线方程的点斜式求得切线方程;
(2)求出原函数的导函数,可得当![]() 时导函数在定义域内大于0恒成立,当a<0时求出导函数的零点,由零点对函数的定义域分段,根据导函数在各区间段内的符号得到函数的单调区间;
时导函数在定义域内大于0恒成立,当a<0时求出导函数的零点,由零点对函数的定义域分段,根据导函数在各区间段内的符号得到函数的单调区间;
(3)令![]() ,求其导函数,得到
,求其导函数,得到![]() ,故
,故![]() ,
, ![]() 从而证得答案.
从而证得答案.
试题解析:
(1)![]() ,
,
故![]() 在
在![]() 处的切线为
处的切线为![]() .
.
(2)![]() ;
;
①当![]() 时,
时, ![]() 恒成立,则
恒成立,则![]() 在
在![]() 上单调递增,
上单调递增,
②当![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(3)先证明: ![]() 时,
时, ![]() ,
,
令![]() ,
,
则![]() 时,
时, ![]() ,
, ![]() 单调递减,故
单调递减,故![]() ,
,
即![]() .
.
故![]() ,
,
令![]()
则![]() (
(![]() ),
),![]()
而![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,
由于![]() ,故
,故![]() ,
,
所以![]() 在
在![]() 内恒成立,故
内恒成立,故![]() 在
在![]() 内单调递增,
内单调递增,
![]() ,
,
所以![]() ,
,
故问题得证.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( ) 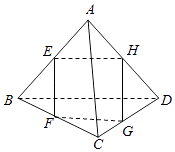
A.2对
B.4对
C.6对
D.8对
查看答案和解析>>
科目:高中数学 来源: 题型:
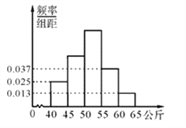
【题目】人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.
(Ⅰ)求该校抽取的学生总数以及第2组的频率;
(Ⅱ)学校为进一步了解学生的身体素质,在第1组、第2组、第3组中用分层抽样的方法抽取6人进行测试.若从这6人中随机选取2人去共同完成某项任务,求这2人来自于同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在对高三学生的4月理科数学调研测试的数据统计显示,全市10000名学生的成绩服从正态分布![]() ,现从甲校100分以上(含100分)的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:
,现从甲校100分以上(含100分)的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:

(注:表中试卷编号![]() )
)
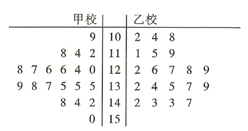
(1)列出表中试卷得分为126分的试卷编号(写出具体数据);
(2)该市又从乙校中也用系统抽样的方法抽取了20份试卷,将甲乙两校这40份试卷的得分制作了茎叶图(如图6),试通过茎叶图比较两校学生成绩的平均分及分散程度(均不要求计算出具体值,给出结论即可);
(3)在第(2)问的前提下,从甲乙两校这40名学生中,从成绩在140分以上(含140分)的学生中任意抽取3人,该3人在全市前15名的人数记为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
(附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com