
分析 (1)根据x=ρcosθ,y=ρsinθ,求出曲线E的普通方程,根据cos2θ+sin2θ=1,求出椭圆C的参数方程即可;
(2)表示出AB的最大值,结合三角函数的性质求出其最大值即可.
解答 解:(1)由x=ρcosθ,y=ρsinθ得:
x2+y2-8y+15=0,即x2+(y-4)2=1,
椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$,
化为参数方程为:$\left\{\begin{array}{l}x=2cosθ\\ y=sinθ\end{array}\right.(θ$为参数).
(2)${|{AB}|_{max}}={|{AE}|_{max}}+1=\sqrt{4{{cos}^2}θ+{{({4-sinθ})}^2}}+1=\sqrt{-3{{sin}^2}θ-8sinθ+20}+1$,
由sinθ∈[-1,1],当sinθ=-1时,|AB|max=6.
点评 本题考查了参数方程和普通方程以及极坐标方程的关系,考查三角函数的性质,是一道中档题.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:选择题
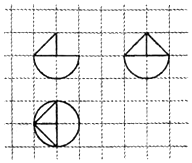
| A. | 3π+$\sqrt{3}$ | B. | 3π+$\sqrt{3}$+1 | C. | 5π+$\sqrt{3}$ | D. | 5π+$\sqrt{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π | B. | 4π | C. | 8π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{39}}{6}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{7}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com